Схема Бернулли. Цепи Маркова

Цепь Маркова — последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что при фиксированном настоящем будущее независимо от прошлого.

Цепи Маркова – одна из основных и актуальных тем в нынешнее время в современной математике. Цепи Маркова являются обобщением схемы Бернулли, которая была написана в XVII, а Марковские цепи получили сравнительно недавно свое признание. Очень много процессов в нынешнее время решаются с помощью схем Бернулли или цепей Маркова. Вся поисковая система Интернета основана на этих процессах.

Эта была одна из основных причин выбора мною этой темы для выпускной квалификационной работы (ВКР). Мне было очень интересно, по какому принципу происходит выборка по рассылке, или по поиску в Интернете. Рассылка спам-ботов основана тоже на этих же процессах.

Цель моей работы – Ознакомиться и как можно подробнее рассмотреть заинтересовавший меня материал. Особенно интересной для меня была эта тема по той причине, что она не рассматривалась в курсе моего обучения в институте, а является частью пройденного материала по теории вероятности.

Свою работу «Приложение схемы Бернулли. Обобщение. Цепи Маркова» я начинаю с введения понятий касающихся раздела схемы Бернулли. Из этого и состоят моя первая глава ВКР - Биография Якоба Бернулли и схема Бернулли. Я рассматриваю различные варианты схем Бернулли, как она по-разному применятся, различные формы записи, обобщения.

Во второй главе своей работы я уже по выше рассмотренным понятиям схем Бернулли ввожу понятие Цепь Маркова, которая была так названа в честь нашего соотечественника, великого математика, Андрея Андреевича Маркова. Для лучшего понятия темы Цепи Маркова в этой главе я рассматриваю введение понятия цепь Маркова с помощью примера.

Третья глава дает нам представление о том, какой объем работы может выполнять человек, который владеет цепями Маркова. Подробно рассматриваю на примере по определению авторства текста. Я посчитал этот пример очень удачным применением Цепей Маркова.

Глава 1. Схема Бернулли

1.1 Исторический курс. Биография Якоба Бернулли

Якоб Бернулли родился 27 декабря 1654 г. По желанию отца готовился к званию протестантского священника. Окончил Базельский университет, где изучал философию, богословие и языки. Владел немецким, французским, английским, итальянским, латинским и греческим языками. Испытывая непреодолимое влечение к математике, изучал ее тайком от отца. В 1671 г. получил степень магистра философии. С большим успехом читал проповеди на немецком и французском языках. В то же время продолжал пополнять свои знания по математике без учителя, почти без учебников.

В октябре 1686 г. оказывается вакантной должность профессора математики в Базельском университете. Успехи Якоба в математике хорошо известны, и Сенат университета единодушно выдвинул на вакантную должность Якоба Бернулли. Вступление в должность состоялось 15 февраля 1687 г. Вряд ли присутствовавшие при этом скромном акте представляли, что они являются свидетелями начала беспримерного в истории математики события: отныне кафедру будут занимать Бернулли на протяжении ста лет. Члены же этой семьи будут профессорами родного университета в течение четверти тысячелетия, вплоть до второй половины XX в.

В том же году Якоб Бернулли прочитал в «Асtа Eruditirum» за 1684 г. «Новый метод» Лейбница и, обнаружив трудные места, письменно обратился к Лейбницу за разъяснением. Лейбниц, находившийся в длительной служебной поездке, получил письмо только через три года, когда надобность в консультации отпала: Якоб совместно Иоганном овладели дифференциальным и интегральным исчислениями настолько, что вскоре смогли приступить систематическому развитию метода. Образовавшийся триумвират — Лейбниц, Якоб и Иоганн Бернулли — менее чем за двадцать лет чрезвычайно обогатил анализ бесконечно малых.

С 1677 г. Я. Бернулли стал вести записные книжки, куда вносил различного рода заметки научного содержания. Первые записи посвящены теологии, сделаны под влиянием распространенного в то время в Базеле сборника спорных теологических вопросов.

Основное место в записных книжках занимает решение задач. Уже по ранним записям можно судить о проявленном Я. Бернулли интересе к прикладной математике. Математические заметки показывают, как постепенно Я. Бернулли овладевал методами Валлиса, Декарта, инфинитезимальными методами, как развивал и совершенствовал их. Решенные им задачи служили отправными пунктами для дальнейших более глубоких исследований.

В январе 1684 г. Я. Бернулли провел в Базельском университете открытый диспут, на котором защищал 100 тезисов, из них 34 логических, 18 диалектических и 48 смешанных. Некоторые тезисы крайне любопытны. Вот примеры:

78. Иногда существует несколько кратчайших путей из точки в точку

83. Среди изопериметрических фигур одна может быть в бесконечное число раз больше другой

85. Не в каждом треугольнике сумма внутренних углов равна двум прямым

89. Квадратура круга еще не найдена, но не потому, что между искривленным и прямолинейным нет никакой связи; в действительности кривую можно спрямить, а криволинейную фигуру квадрировать

В мае 1690 г. Я. Бернулли опубликовал в «Асtа Eruditirum» первую работу, связанную с исчислением бесконечно малых. В ней он дал решение поставленной Лейбницем в 1687 г. задачи о парацентрической изохроне. Необходимо было найти кривую, по которой материальная точка опускалась бы в равные промежутки времени на равные высоты. Я. Бернулли вывел дифференциальное уравнение кривой и проинтегрировал его. При этом он впервые употребил в печати термин «интеграл», указав, что из равенства двух выражений, связывающих дифференциалы, следует равенство интегралов.

В лекциях, читанных Лопиталю, И. Бернулли ход решения излагает так. Пусть искомой кривой будет АDС. Материальная точка за время ∆t перемещается из точки D в точку d и из точки С в точку с. По условию задачи проекции дуг Dd Сс на вертикаль одинаковы. Проведем через D и С касательные к кривой до пересечения с продолжением АF. Отрезки касательных будут DK и CL. Напишем тождество

Вв.Сс=Вв.Рс • Рс.Ссю

Дуги Dd и Сс малы, поэтому фигуры GDd и НСс можно считать треугольниками.

Из подобия треугольников GDd и DEK, НСс и СFL получим

Вв.ВП=ВЛ.ВУбСс.Нс=СД.САю

С помощью этих пропорций найдем

Вв.Сс=ВП1Нс • ВК.ВЕ • СА.СДю

По условиям задачи dG/Нс=1, поэтому

Вв1Сс=ВК.ВЕ • СА.СДю

Проведем через точку С прямую СМ, параллельную DК. Тогда

DК/DЕ=СМ/СF, Dd/Сс=СМ/СL.

Но отношение Dd/Сс равно отношению скоростей (интервал ∆t один и тот же), квадраты же скоростей, по найденному Галилеем закону, относятся как пройденные высоты; это дает

Dd²/Сс²=СМ²/СL²=DЕ/CF, СМ²/СL² =DЕ/СF.

Последнее равенство означает, что если через две произвольные точки кривой провести касательные СL и DК и через точку С провести СМ параллельно DК, то должна выполняться указанная пропорция. Таким свойством обладает искомая кривая.

Задача оказалась сведенной к классу обратных задач на касательные: найти кривую, касательные к которой удовлетворяют некоторому требованию. Подобную задачу впервые предложил Декарту Дебон, и Декарт с ней не справился. Разработанный Лейбницем метод позволяет решать и обратные задачи на касательные.

Выберем начало координат в точке А. Обозначим АЕ=х, ЕD=у. Тогда GD=dх, Gd=dу. Обозначим также СF=а, СL=b. Треугольники FСМ и СdD подобны, отсюда

Gd/Dd=FС/СМ.

Но Dd = √dx²+dy², поэтому

dy/√ dx²+dy²= а/СМ, откуда

CM²= (a²dx²+a²dy²)/dy².

Подставим найденное выражение в пропорцию СL²/СM²=СF/СЕ и получим дифференциальное уравнение

и²вн².(ф²вч²+ф²вн²)=ф.нб и²нвн²-ф³вн²=ф³вч²б (и²н-а³)ву² = а³вч²б

√b²y-a³ dy=√a³dx.

В уравнении переменные разделены, интегрирование его дает искомую кривую

2b²у — 2а³/3b² √b²у - а³ == х√а³.

Парацентрическая изохрона оказалась полукубической параболой. Вид кривой раньше Я. Бернулли определили Лейбниц и Гюйгенс, но лишь Я. Бернулли дал решение средствами анализа бесконечно малых.

В приложении к другой работе о рядах (1694 г.) Я. Бернулли сформулировал несколько тезисов.

1. Существуют спирали, которые совершают бесконечное число витков вокруг полюса, но имеют конечную длину.

2. Существуют кривые, которые, подобно эллипсу, замкнуты и, подобно параболе, уходят в бесконечность, например ay²=х²(b+х).

3. Существуют кривые, состоящие из двух ветвей, например ау²=х(а²—х²),

4. Существуют неограниченные поверхности с конечной площадью.

5. Существуют неограниченные поверхности с бесконечной площадью, но такие, что соответствующие им тела вращения обладают конечным объемом.

Я. Бернулли увлекался также и изопериметрическими задачами. Древнейшая из них—задача легендарной основательницы Карфагена и его первой царицы Дидоны. Легенда такова. Дидона бежала от отца, тирского царя, и достигла Африки, где купила у туземцев участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Она разрезала шкуру на узкие полоски и связала из них длинную ленту. Спрашивается, какой формы должна быть фигура, оцепленная лентой данной длины, чтобы площадь фигуры была наибольшей?

Ван-дер-Варден пишет, что Зенодор, живший вскоре после Архимеда, высказал 14 предложений относительно изопериметрических фигур. Он утверждал, что из всех фигур (кругов и многоугольников), имеющих одинаковый периметр, круг будет наибольшим, а также и то, что из всех пространственных тел с одинаковой поверхностью наибольшим будет шар.

Решение задачи содержится в записных книжках Я. Бернулли и помещено в майском номере «Acta Eruditorum» за 1701 г. Я. Бернулли и здесь применил высказанный ранее принцип: поскольку площадь должна быть экстремальной, этим же свойством должна обладать и любая ее элементарная часть. Он получил дифференциальное уравнение третьего порядка и впоследствии проинтегрировал его.

К.А. Рыбников пишет: «Таким образом, решение изопериметрической задачи означало очень важный, принципиально новый этап в истории вариационного исчисления; оно дало возможность решать более сложные вариационные задачи, им был сделан важный шаг на пути решения вариационных задач».

При изучении свойств сочетаний и фигурных чисел Я. Бернулли встретился с суммированием степеней натуральных чисел Sm = å km

Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы сумм от S(n) до S(n¹⁰):

S (n) = n²/2 +n/2

S (n²) = n³/3 + n²/2+ n/6

S (n³) = n⁴/4 + n³/2 + n2/4

S (n⁴) = n⁵/5 + n⁴/2 + n³/3 – n/30

S (n⁵) = n⁶/6 + n⁵/2 + 5n⁴/12 - n²/12

S (n⁶) = n⁷/7 + n⁶/2 + n⁵/2 - n³/6 + n/42

S (n⁷) = n⁸/8 + n⁷/2 + 7n⁶/12 - 7n⁴/24 + n²/12

S (n⁸) = n⁹/9 + n⁸/2 + 2n⁷/3 - 7n⁵/15 + 2n³/9 – n/30

S (n⁹) = n¹⁰/10 + n⁹/2 + 3n⁸/4 - 7n⁶/10 + n⁴/2 - n²/12

S (n¹⁰) = n¹¹/11 + n¹⁰/2 + 5n⁹/9 – n⁷ + n⁵ - n³/2 + 5n/66

Затем Я. Бернулли указал общую формулу

S(nc) = n^c+1/c+1 + 1/2*n^c + 1/2*( )An^c-1 + 1/4*( )Bn^c-3 + 1/6*( )Cn^c-5 +

+1/8*( )Dn^c^-7+ …

Здесь ( ), ( ) … - числа сочетаний; показатели степени n убывают, последний член в правой части содержит n или n².

Числа A, B, C, D … - коэффициенты при n в выражениях S(n²), S(n⁴), S(n⁶), …

Именно: А=1/6, В=-1/30, С=1/42, D=-1/30,

Бернулли формулирует общее правило для вычисления этих чисел: сумма коэффициентов в выражениях S(n), S(n²), S(n³), … равна единице. Например, 1/9+1/2+2/3-7/15+2/9+D=1. Отсюда D=-1/30.

Я. Бернулли подчеркивает удобство таблицы фигурных чисел и заявляет, что с ее помощью в течение «половины четверти часа» нашел сумму десятых степеней первой тысячи натуральных чисел. Она оказалась равной

91 409 924 241 424 243 424 241 924 242 500.

1.2 Схема Бернулли. Обобщение

Определение 1. Схемой Бернулли называется последовательность независимых в совокупности испытаний, в каждом из которых возможны лишь два исхода - "успех" и "неудача", при этом успех в одном испытании происходит с вероятностью $Описание: p\in (0,\,1),$ а неудача - с вероятностью .

Под независимостью в совокупности испытаний понимается независимость в совокупности любых событий, относящихся к разным испытаниям. В испытаниях схемы Бернулли, когда с одним испытанием можно связать только два взаимоисключающих события, независимость в совокупности испытаний означает, что при любом независимы в совокупности события $Описание: A_1=\{$ успех в первом испытании $Описание: \},\, \dots,\,A_{n}=\{$ успех в -м испытании $Описание: \}$ . Эти события принадлежат одному и тому же пространству элементарных исходов, полученному декартовым произведением бесконечного числа двухэлементных множеств $Описание: \{\textit{у,\,н\/}\}$ :

$Описание: \Omega=\{(a_1,\,a_2,\,\ldots\,) {\hspace{3pt}{\left|\right.}\mspace{1mu}} a_i\in\{\textit{у,\,н\/}\}\}.$

Здесь буквами "у" и "н" обозначены успешный и неудачный результаты испытаний соответственно.

Обозначим через $Описание: \nu_n$ число успехов, случившихся в испытаниях схемы Бернулли. Эта величина может принимать целые значения от нуля до в зависимости от результата испытаний. Например, если все испытаний завершились неудачей, то величина $Описание: \nu_n$ равна нулю.

Теорема 1 (формула Бернулли). При любом $Описание: k=0,\,1,\,\ldots,\,n$ имеет место равенство:

$Описание: \Prob(\nu_n=k)=C^k_n p^k q^{n-k}.$

Доказательство. Событие $Описание: A=\{\nu_n=k\}$ означает, что в испытаниях схемы Бернулли произошло ровно успехов. Рассмотрим один из благоприятствующих событию элементарных исходов:

$Описание: (\underbrace{\textit{у,\, у,\, \ldots,\, у}}_k ,\,\underbrace{\textit{н,\,н,\, \ldots,\, н}}_{n-k}),$

когда первые испытаний завершились успехом, остальные неудачей. Поскольку испытания независимы, вероятность такого элементарного исхода равна $Описание: p^k q^{n-k}$ . Другие благоприятствующие событию элементарные исходы отличаются лишь расположением успехов на местах. Есть ровно способов расположить успехов на местах. Поэтому событие состоит из элементарных исходов, вероятность каждого из которых также равна $Описание: p^k q^{n-k}$ .

Определение 2. Набор чисел $Описание: \bigl\{C_n^k p^k q^{n-k},\, k=0,\,1,\,\dots,\,n\bigr\}$ называется биномиальным распределением вероятностей.

1.2.1 Номер первого успешного испытания

Рассмотрим схему Бернулли с вероятностью успеха в одном испытании. Введем величину $Описание: \tau$ со значениями $Описание: 1,\,2,\,3,\,\dots,$ равную номеру первого успешного испытания.

Теорема 2. Вероятность того, что первый успех произойдет в испытании с номером $Описание: k\in\mathbb N=\{1,2,3,\ldots\},$ равна

$Описание: \Prob(\tau=k)=p\mspace{2mu}q^{k-1}$ .

Доказательство. Вероятность первым испытаниям завершиться неудачей, а последнему - успехом, равна

$Описание: \qquad_\Prob(\tau=k)=\Prob_(\textit{н,\, \dots,\, н},\,\textit{ у})=p\mspace{2mu}q^{k-1}. \qquad$

Определение 3. Набор чисел $Описание: \{p\mspace{2mu}q^{k-1},\, k=1,\,2,\,3,\,\dots\}$ называется геометрическим распределением вероятностей.

Геометрическое распределение вероятностей обладает интересным свойством, которое можно назвать свойством "нестарения".

Теорема 3. Пусть $Описание: \Prob(\tau=k)=p\mspace{2mu}q^{k-1}$ для любого $Описание: k\in\mathbb N$ . Тогда для любых неотрицательных целых и имеет место равенство:

$Описание: \Prob(\tau>n+k {\hspace{3pt}{\left|\right.}\mspace{1mu}} \tau>n) = \Prob(\tau>k).$

Если, например, считать величину $Описание: \tau$ временем безотказной работы (измеряемым целым числом часов) некоторого устройства, то данному равенству можно придать следующее звучание: вероятность работающему устройству проработать еще сколько-то часов не зависит от того момента, когда мы начали отсчет времени, или от того, сколько уже работает устройство. Общепринятое название этого свойства - свойство отсутствия последействия.

Доказательство. По определению условной вероятности,

$Описание: \begin{equation}_\Prob(\tau>n+k {\hspace{3pt}{\left|\right.}\mspace{1mu}} \tau>n)=\frac{\Prob(\tau>n+k,\, \tau>n)}{\Prob(\tau>n)}=_\frac{\Prob(\tau>n+k)}{\Prob(\tau>n)}._\end{equation}$

(1)

Последнее равенство следует из того, что событие $Описание: \{\tau>n+k\}$ влечет событие $Описание: \{\tau>n\},$ поэтому пересечение этих событий есть $Описание: \{\tau>n+k\}$ . Найдем для целого $Описание: m\ge 0$ вероятность $Описание: \Prob(\tau>m)$ :

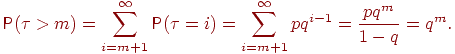
$Описание: \Prob(\tau>m)=\sum_{i=m+1}^\infty \Prob(\tau=i)=_\sum_{i=m+1}^\infty p q^{i-1}=\frac{ p q^m}{1-q}=q^m.$

Можно получить $Описание: \Prob(\tau>m)$ еще проще: событие $Описание: \{\tau>m\}$ означает в точности, что в схеме Бернулли первые испытаний завершились неудачами, т.е. его вероятность равна . Возвращаясь к (1), получим

$Описание: \Prob(\tau>n+k {\hspace{3pt}{\left|\right.}\mspace{1mu}}_\tau>n)=\frac{\Prob(\tau>n+k)}{\Prob(\tau>n)}=_\frac{q^{n+k}}{q^n}=q^k=\Prob(\tau>k).$

Теорема 3 доказана.

1.2.2 Независимые испытания с несколькими исходами

Рассмотрим схему независимых испытаний уже не с двумя, а с большим количеством возможных результатов в каждом испытании.

Пример 1. Игральная кость подбрасывается 15 раз. Найти вероятность того, что выпадет ровно десять троек и три единицы.

Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани. Поэтому воспользоваться формулой для числа успехов в схеме Бернулли не удаcтся.

Попробуем вывести подходящую формулу. Пусть в одном испытании возможны исходов: $Описание: 1,\,2,\,\dots,\,m$ , и -й исход в одном испытании случается с вероятностью , где $Описание: p_1+\ldots+p_m=1$ .

Обозначим через $Описание: P(n_1,\,\dots,\,n_m)$ вероятность того, что в независимых испытаниях первый исход случится раз, второй исход - раз, и т.д., наконец, -й исход - раз.

Теорема 4 (Обобщенная формула Бернулли). Для любого и любых неотрицательных целых чисел $Описание: n_1,_\ldots, n_m,$ сумма которых равна верна формула

$Описание: P(n_1,\,\ldots,\,n_m)=_\frac{n!}{n_1!\,\ldots\, n_m!}\, {\mathstrut p}_1^{n_1}\cdot\ldots\cdot _{\mathstrut p}_m^{n_m}.$

Доказательство. Рассмотрим один элементарный исход, благоприятствующий выпадению единиц, двоек и т.д.:

$Описание: (\underbrace{1,\,\ldots,\,1}_{n_1},\,\underbrace{2,\,\ldots,\,2}_{n_2},\,_\ldots, \underbrace{m,\,\ldots,\,m}_{n_m}).$

Это результат экспериментов, когда все нужные исходы появились в некотором заранее заданном порядке. Вероятность такого результата равна произведению вероятностей $Описание: {\mathstrut p}_1^{n_1}\cdot\ldots\cdot {\mathstrut p}_m^{n_m}$ . Остальные благоприятные исходы отличаются лишь расположением чисел $Описание: {1,\,2,\,\ldots,\,m}$ на местах. Число таких исходов равно числу способов расположить на местах единиц, двоек, и т.д. Это число равно

$Описание: C_{n}^{n_1}\cdot C_{n-n_1}^{n_2}\cdot_C_{n-n_1-n_2}^{n_3}\cdot\ldots_\cdot C_{n-n_1-\ldots-n_{m-1}}^{n_m}= _ \frac{n!}{n_1!\,\ldots\,n_m!}\,._$

Теперь мы можем вернуться к примеру 1 и выписать ответ: вероятность получить десять троек, три единицы и еще два других очка равна

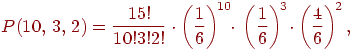
$Описание: P(10,\,3,\,2)=\frac{15!}{10! 3! 2!}\cdot\left(\frac{1}{6}\right)^{\!10}_\!\!\cdot\,\left(\frac{1}{6}\right)^{\!3}\!\cdot_\left(\frac{4}{6}\right)^{\!2},$

так как вероятности выпадения тройки и единицы равны по , а вероятность третьего исхода (выпала любая другая грань) равна $Описание: 4/ 6{\text.}$

1.2.3 Теорема Пуассона для схемы Бернулли

Предположим, нам нужна вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха . Вероятность этого события равна любому из следующих выражений, вычислить которые довольно сложно:

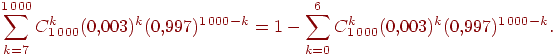
$Описание: \sum\limits_{k=7}^{1\,000}C_{1\,000}^k (0{,}003)^k (0{,}997)^{1\,000-k} =1-\sum\limits_{k=0}^6 C_{1\,000}^k (0{,}003)^k (0{,}997)^{1\,000-k}.$

Сформулируем теорему о приближенном вычислении вероятности иметь успехов в большом числе испытаний Бернулли с маленькой вероятностью успеха . Термин "большое число" должен означать $Описание: n\to\infty$ . Если при этом остается неизменной, то вероятность получить любое заданное число успехов уменьшается до нуля. Необходимо чтобы вероятность успеха уменьшалась одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность успеха меняться не может (см. определение схемы Бернулли). Поэтому нам придется рассмотреть так называемую "схему серий": если испытание одно, то вероятность успеха в нем равна если испытаний два, то вероятность успеха в каждом равна и т.д. Если испытаний то в каждом из них вероятность успеха равна . Вероятность успеха меняется не внутри одной серии испытаний, а от серии к серии, когда меняется общее число испытаний. Обозначим через $Описание: \nu_n$ число успехов в -й серии испытаний.

Теорема 5 (теорема Пуассона). Пусть $Описание: n\to\infty$ и $Описание: p_n\to 0$ так, что $Описание: n p_n \to\lambda >0$ Тогда для любого $Описание: k\ge 0$ вероятность получить успехов в испытаниях схемы Бернулли с вероятностью успеха стремится к величине $Описание: {\lambda^k} e^{-\lambda}\,/\,{k!}$

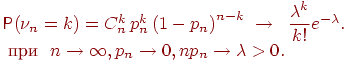
$Описание: \Prob(\nu_n=k)=C_n^k\,p_n^k\,{(1-p_n)}^{n-k} \; \to \;\;\dfrac{\lambda^k}{k!} e^{-\lambda}. \\ \text{ при } \n\to\infty, p_n\to 0, np_n \to \lambda>0.$

Доказательство. Положим $Описание: \lambda_n=n p_n$ . По условию $Описание: \lambda_n\to\lambda>0$ . Подставим $Описание: p_n=\lambda_n/n$ в формулу Бернулли:

$Описание: \begin{multiline} \qquad \displaystyle C_n^k\, p_n^k\, (1-p_n)^{n-k}=\,C_n^k\,\dfrac{\lambda_n^k}{n^k}\,\left(1-\frac{\lambda_n}{n}\right)^{n-k}=\\=\underbrace{\dfrac{n(n\mspace{1mu}{-}\mspace{1mu}1)\ldots(n\mspace{1mu}{-}\mspace{1mu}k\mspace{1mu}{+}\mspace{1mu}1)}{n^k}}_{\begin{array}{c}\downarrow\cr 1\end{array}}\, \dfrac{\lambda_n^k}{k!} \,\underbrace{\left(1-\frac{\lambda_n}{n}\right)^n}_{\begin{array}{c}\downarrow\cr e^{-\lambda}\end{array}}\,\underbrace{\left(1-\frac{\lambda_n}{n}\right)^{-k}}_{\begin{array}{c}\downarrow\cr 1\end{array}}\longrightarrow\frac{\lambda^k}{k!}~e^{-\lambda}. \ \label{eq5-2}\end{multiline}\vskip -2pt$

(2)

В соотношении (2) мы воспользовались тем, что $Описание: \lambda_n^k\to\lambda^k$ и замечательным пределом $Описание: \left(1-{\lambda_n}\mspace{1mu}/\mspace{1mu}{n}\right)^n \toe^{-\lambda}$ . Докажем последнее свойство:

$Описание: \quad\ln{\left(1-\frac{\lambda_n}{n}\right)}^n=n \ln {\left(1-\frac{\lambda_n}{n}\right)}=n \left(-\frac{\lambda_n}{n} +O\left(\frac{\lambda_n^2}{n^2}\right)\right)\to -\lambda. \quad$

Определение 4. Набор чисел $Описание: \Bigl\{\frac{\lambda^k}{k!} e^{-\lambda}, \k=0,\,1,\,2,\,\dots\,\Bigr\}$ называется распределением Пуассона с параметром $Описание: \lambda>0$ .

По теореме 17 можно приближенно посчитать вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха с вычисления которой мы начали. Поскольку $Описание: {n=1\,000}$ "велико", а $Описание: p_n=0{,}003$ "мало", то, взяв $Описание: \lambda=np_n=3,$ можно записать приближенное равенство

$Описание: \begin{equation}1-\sum_{k=0}^6 C_{1\,000}^k (0{,}003)^k (0{,}997)^{1\,000-k}\approx 1-\sum_{k=0}^6 \frac{3^k}{k!} e^{-3}\approx 0{,}034. \ \label{eq5-3}\end{equation}$ (3)

Осталось решить, а достаточно ли велико, а $Описание: p_n=0{,}003$ мало, чтобы заменить точную вероятность на ее приближенное значение. Для этого нужно уметь оценивать разницу между этими вероятностями.

Следующую очень полезную теорему мы, исключительно из экономии времени, доказывать не станем.

Теорема 6 (уточненная теорема Пуассона). Пусть - произвольное множество целых неотрицательных чисел, $Описание: \nu_n$ - число успехов в испытаниях схемы Бернулли с вероятностью успеха $Описание: \lambda=np$ . Cправедливо неравенство

$Описание: \biggl|\Prob(\nu_n\in A) - \sum_{k\in A}\frac{\lambda^k}{k!} e^{-\lambda}\biggr| =\\\biggl|\sum_{k\in A} C_n^k p^k (1-p)^{n-k} -\sum_{k\in A} \frac{\lambda^k}{k!} e^{-\lambda}\biggr| \le\min(p,\,np^2).$

Таким образом, теорема 6 предоставляет нам возможность самим решать, достаточно ли велико, а мало, руководствуясь полученной величиной погрешности. Какова же погрешность в формуле (3)? Взяв $Описание: A=\{0,\,1,\,\dots,\,6\}$ имеем

$Описание: \begin{multiline*}\bigl |\, \Prob (\nu_{1000}\ge 7)- 0{,}034\, \bigr |=\biggl |\, \Bigl (1-\Prob (\nu_{1000}\le 6)\Bigr ) -\Bigl (1-\sum_{k=0}^6 \frac{3^k}{k!} e^{-3}\Bigr)\, \biggr| = \\ =\biggl |\, \Prob (\nu_{1000}\le 6) -\sum_{k=0}^6 \frac{3^k}{k!} e^{-3}\, \biggr | \le \min(p,\, np^2) = 0{,}003. \qquad\end{multiline*}$

Таким образом, можно утверждать, что искомая вероятность заключена в границах $Описание: (0,034 - 0,003, \; 0,034 + 0,003) = (0,031, \; 0,037)$ .

Пример 2. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Решение. Событие А – достали белый шар. Тогда вероятности, . По формуле Бернулли требуемая вероятность равна

Описание: image012 .

Пример 3. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

Решение. Вероятность рождения девочки , тогда .

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:

, ,

, .

Следовательно, искомая вероятность

Пример 4. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.

Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность , тогда . Отсюда по формуле Бернулли находим.

Пример 5. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.

Решение. Вычисляем по формуле Бернулли:

Пример 6. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n < k), если в каждом из них .

Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:

D – в n-ом испытании А произошло;

С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.

Теорема умножения и формула Бернулли дают требуемую вероятность:

цепь марков бернулли информатика

Глава 2. Цепи Маркова

2.1 Биография Маркова

Марков Андрей Андреевич. 2 (14) июня 1856—20 июля 1922 — русский математик, специалист по теории чисел, теории вероятностей и математическому анализу.

С 1886 — адъюнкт, с 1890 — экстраординарный, а с 1896 — ординарный академик Императорской Санкт-Петербургской Академии Наук.

Андрей Марков родился в семье мелкого чиновника в Рязанской губернии. В 1878 окончил Петербургский университет со степенью кандидата и в том же году получил золотую медаль за работу "Об интегрировании дифференциальных уравнений при помощи непрерывных дробей". С 1880 — приват-доцент, с 1886 — профессор, а с 1905 — заслуженный профессор Петербургского университета.

Научные исследования Марков тесно примыкают по своей тематике к работам старших представителей Петербургской математической школы — П.Л. Чебышева, Е.И. Золотарева и А.Н. Коркина. Блестящих результатов в области теории чисел Марков достиг в магистерской диссертации "О бинарных квадратичных формах положительного определителя" (1880). Результаты, полученные им в этой работе, послужили основой дальнейших исследований в этой области в СССР и за рубежом. В 1905 вышел в отставку. В этом же году ему присвоено звание заслуженного профессора Петербургского университета. Написал около 70 работ по теории чисел, теории приближения функций, теории дифференциальных уравнений, теории вероятностей, в т. ч. и 2 классических произведения — "Исчисление конечных разностей" и "Исчисление вероятностей". Труды Маркова по теории чисел касаются главным образом теории неопределенных квадратичных форм. Почти все они посвящены нахождению экстремальных квадратичных форм данного определителя.

Марков внес важный вклад в своеобразную область геометрии чисел, которая в настоящее время интенсивно развивается. Обогатил важными открытиями и методами также теорию вероятностей: развил метод моментов П.Л. Чебышева настолько, что стало возможным доказательство центральной предельной теоремы, существенно расширил сферу применения закона больших чисел и центральной предельной теоремы, распространив их не только на независимые, но и на зависимые опыты.

В цикле работ, опубликованных в 1906-1912, заложил основы одной из общих схем естественных процессов, которые можно изучать методами математического анализа. Впоследствии эта схема была названа цепями Маркова и привела к развитию нового раздела теории вероятностей — теории случайных процессов, которые играют важную роль в современной науке. В качестве примера случайных процессов можно назвать диффузию газов, химические реакции, лавинные процессы и т. д. Важное место в творчестве Маркова занимают вопросы математической статистики. Он вывел принцип, эквивалентный понятиям несмещенных и эффективных статистик, которые получили теперь широкое применение.

В математическом анализе Марков развил теорию моментов и теорию приближения функций, а также аналитическую теорию непрерывных дробей. Ученый широко использовал непрерывные дроби для приближенных вычислений в теории конечных разностей, интерполировании и т. д. Актуальность всех этих вопросов особенно возросла в связи с развитием вычислительной техники. Марков пользовался большим авторитетом среди студентов.

Он был материалистом и убежденным атеистом, бескомпромиссным борцом против религии. 12.02.1912 Марков подал в Синод прошение об отлучении его от церкви. Марков протестовал против решения царского правительства, отказывавшегося утвердить избрание А.М. Горького почетным членом Петербургской Академии Наук. АН СССР учредила премию им. А.А. Маркова за лучшие работы по математике. Именем Маркова назван кратер краевой зоны Луны.

Свой последний мемуар он представил Академии наук всего лишь за несколько месяцев до смерти. Тяжелый недуг свалил его в постель, и 20 июля 1922 г. он умер.

2.2 Цепи Маркова

Определение 5. Процесс, протекающий в физической системе, называется марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.

Определение 6. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий A_i из полной группы. При этом условная вероятность p_ij(s) того, что в s –ом испытании наступит событие A_j при условии, что в (s – 1) – ом испытании наступило событие A_i, не зависит от результатов предшествующих испытаний.

Независимые испытания являются частным случаем цепи Маркова. События называются состояниями системы, а испытания – изменениями сос