Методы интегрирования
Федеральное агентство по образованию
Государственное общеобразовательное учреждение высшего профессионального образования
Калмыцкий Государственный Университет
Лабораторный практикум для студентов
факультета математики и физики
Методы интегрирования
Элиста 2006
ЛАБОРАТОРНАЯ РАБОТА №1
Первообразная. Неопределенный интеграл
Опр1. Пусть функция ![]() определена на некотором конечном или бесконечном промежутке
определена на некотором конечном или бесконечном промежутке ![]() числовой оси R. Функция
числовой оси R. Функция ![]() , определенная на этом промежутке, называется первообразной функцией (или просто первообразной) функции
, определенная на этом промежутке, называется первообразной функцией (или просто первообразной) функции ![]() на
на ![]() , если
, если
функция ![]() непрерывна на
непрерывна на ![]() ;
;
во всех внутренних токах x промежутка ![]() функция
функция ![]() имеет производную и
имеет производную и ![]() ;
;
Пример1. Пусть ![]() . Тогда функция
. Тогда функция ![]() , является первообразной для
, является первообразной для ![]() так как:
так как:
функция ![]() определена на области определения функции
определена на области определения функции ![]() (т.е. на R);
(т.е. на R);
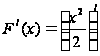 =
=![]() =
=![]()
![]() .
.
Заметим, что функции вида ![]()
![]() ,
, ![]() и им подобные также являются первообразными для функции
и им подобные также являются первообразными для функции ![]() , т. к.
, т. к.
Функции ![]()
![]() ,
, ![]() непрерывны на R (области определения функции
непрерывны на R (области определения функции![]() );
);
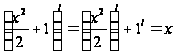 ;
; 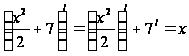 .
.
Таким образом, если ![]() - первообразная функции
- первообразная функции ![]() на промежутке
на промежутке ![]() , то для любой постоянной
, то для любой постоянной ![]() функция
функция ![]() тоже является первообразной функции
тоже является первообразной функции ![]() на
на ![]() .
.
Опр 2. Совокупность всех первообразных функции ![]() , определенной на некотором промежутке
, определенной на некотором промежутке ![]() , называется неопределенным интегралом функции
, называется неопределенным интегралом функции ![]() на этом промежутке и обозначается
на этом промежутке и обозначается ![]() . Символ
. Символ ![]() называется знаком интеграла,
называется знаком интеграла, ![]() - подынтегральной функцией.
- подынтегральной функцией.
Если ![]() какая-либо первообразная функции
какая-либо первообразная функции ![]() на
на ![]() , то пишут
, то пишут ![]() .
.
Основные свойства неопределенного интеграла:
Пусть функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() и дифференцируема в его внутренних точках, тогда
и дифференцируема в его внутренних точках, тогда ![]() или, что тоже самое
или, что тоже самое ![]() .
.
Пусть функция ![]() имеет первообразную на промежутке
имеет первообразную на промежутке![]() , тогда для любой внутренней точки промежутка
, тогда для любой внутренней точки промежутка ![]() имеет место равенство
имеет место равенство ![]() или, что то же
или, что то же ![]() .
.
Если функции ![]() и
и ![]() имеют первообразные на
имеют первообразные на ![]() , то и функция
, то и функция ![]() также имеет первообразную на
также имеет первообразную на ![]() , причем
, причем ![]() .
.
Обобщение: .
.
Если функция ![]() имеет первообразную на промежутке
имеет первообразную на промежутке ![]() и
и ![]() – число, то функция
– число, то функция ![]() также имеет на
также имеет на ![]() первообразную, причем при
первообразную, причем при ![]() справедливо равенство
справедливо равенство ![]()
Таблица основных интегралов
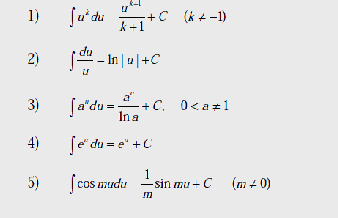
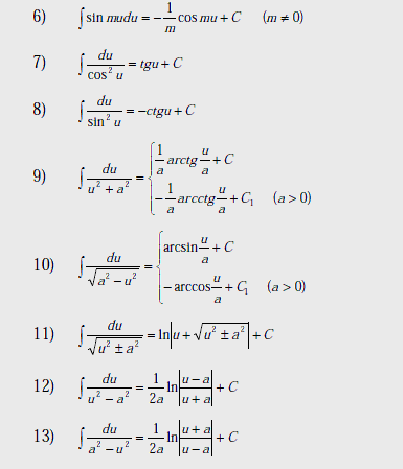
Таблица дифференциалов:
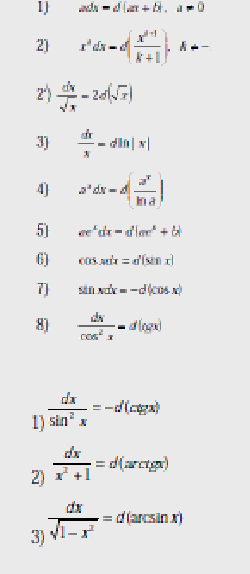
Вообще
![]()
Этой таблицей можно пользоваться.
Так, например, выражение ![]() мы будем представлять в виде
мы будем представлять в виде ![]() или выражения
или выражения ![]() в виде
в виде ![]() и говорить, что подводим функцию
и говорить, что подводим функцию ![]() или
или ![]() , соответственно, под знак дифференциала.
, соответственно, под знак дифференциала.
Замечание: ![]() .
.
Интегралы, получающиеся из табличных «линейным сдвигом» аргумента (т.е. интегралы вида ![]() ,
, ![]() ,
, ![]() ,…) будем называть почти табличными интегралами.
,…) будем называть почти табличными интегралами.
Пример2.
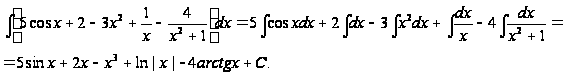
Варианты
Вычислить интегралы:
В-1

В-2
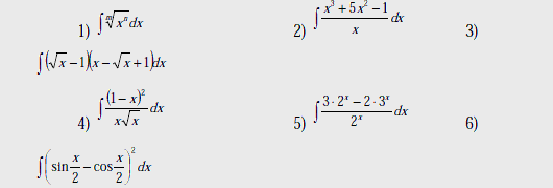
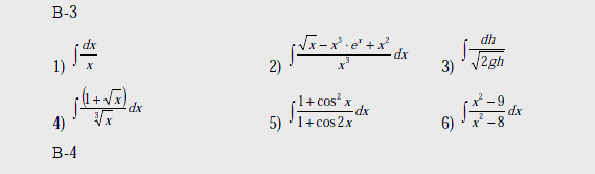

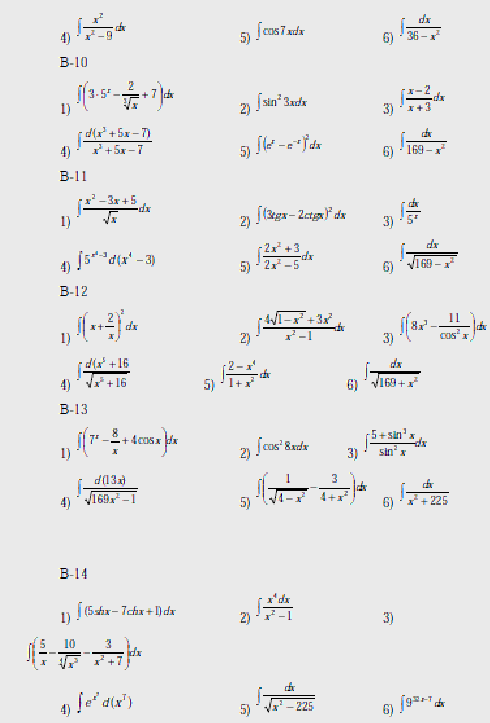


Вопросы к лабораторной работе №1
Дайте определение первообразной функции или интеграла от заданной функции ![]() в заданном промежутке.
в заданном промежутке.
Какова общая формула записи всех первообразных от заданной функции ![]() ?
?
Что называется неопределенным интегралом от ![]() ; как он обозначается? Что такое подынтегральное выражение и подынтегральная функция?
; как он обозначается? Что такое подынтегральное выражение и подынтегральная функция?
Сформулируйте свойства неопределенного интеграла, непосредственно вытекающие из его определения.
В чем разница между выражениями: ![]() и
и ![]() ?
?
Рассмотрите таблицу основных интегралов. Покажите, как каждая из ее формул получается из соответствующей формулы для производной.
Докажите, что ![]() , где
, где ![]() - постоянная, не равная нулю.
- постоянная, не равная нулю.
Чему равен неопределенный интеграл от суммы дифференциалов?
Чему равен интеграл ![]() , если известно, что
, если известно, что ![]() ?
?
ЛАБОРАТОРНАЯ РАБОТА №2
Методы интегрирования (Замена переменной. Интегрирование по частям)
Замена переменной
Пусть функции ![]() и
и ![]() определены соответственно на промежутках
определены соответственно на промежутках ![]()
и ![]() ; функция
; функция ![]() непрерывна на промежутке
непрерывна на промежутке![]() и дифференцируема в его внутренних точках. Тогда, если функция
и дифференцируема в его внутренних точках. Тогда, если функция ![]() имеет первообразную
имеет первообразную ![]() на
на ![]() и, следовательно,
и, следовательно, ![]() то функция
то функция ![]() имеет на
имеет на ![]() первообразную
первообразную ![]() и поэтому
и поэтому ![]()
Замечание: то есть, полагаем ![]() ;
;
Пример 1: Вычислить ![]() . Делаем замену
. Делаем замену ![]() .
.
Тогда ![]()
![]() .
.![]()
Пример 2: Вычислить ![]() Делаем замену
Делаем замену ![]()
![]() ,
,
Тогда ![]()
Интегрирование по частям.
Если функции ![]() и
и ![]() непрерывны на некотором промежутке, дифференцируемы в его внутренних точках и на этом промежутке существует интеграл
непрерывны на некотором промежутке, дифференцируемы в его внутренних точках и на этом промежутке существует интеграл ![]() , то на нем существует и интеграл
, то на нем существует и интеграл![]() причем
причем ![]()
Пример 3
Вычислить ![]() Полагаем
Полагаем ![]() Тогда
Тогда ![]()
Обычно в интегралах вида
![]()
![]() в качестве u берется
в качестве u берется ![]() , где
, где ![]() - многочлен степени
- многочлен степени ![]()
![]()
В интегралах вида

в качестве ![]() берутся
берутся ![]() ,
, ![]() -многочлен степени
-многочлен степени ![]()
3) Интегралы вида
![]()
В интегралы указанного вида входит выражение ![]() , которое называют квадратным трехчленом.
, которое называют квадратным трехчленом.
Всякий квадратный трехчлен, у которого коэффициент при х в первой степени равен нулю, называется каноническим.
Он имеет вид ![]() .
.
Покажем на примерах, как квадратный трехчлен приводится к каноническому виду.
Пусть дан трехчлен ![]() . Дополняем его до полного квадрата. Чтобы избежать дробных слагаемых, поступаем так:
. Дополняем его до полного квадрата. Чтобы избежать дробных слагаемых, поступаем так:
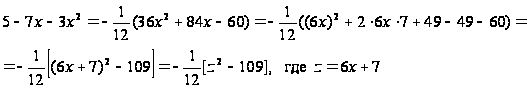
Тогда
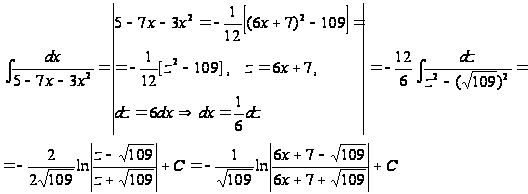
Варианты
Вычислить интегралы:


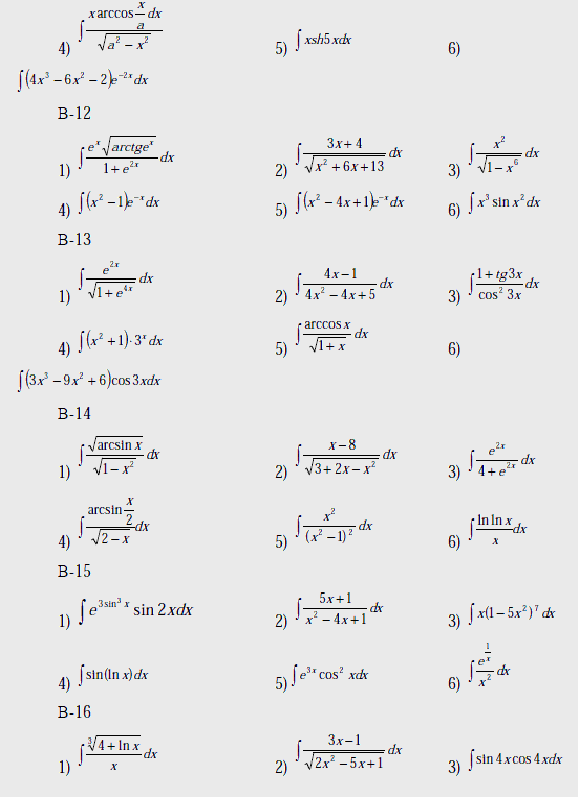


Вопросы к лабораторной работе №2
На каком свойстве дифференциала основан метод замены переменной или подстановки?
При каких условиях этот метод применим?
Покажите, что правило интегрирования по частям есть следствие правила дифференцирования произведения функций.
Назовите классы интегралов, которые можно вычислить интегрированием по частям.
Как вычисляются интегралы вида ![]() ,
, ![]() ,
, ![]() , где
, где ![]() - многочлен целой степени относительно х?
- многочлен целой степени относительно х?
В чем особенности вычисления интегралов:
![]() ,
, ![]() ?
?
Выведите рекуррентную формулу для вычисления интеграла
![]()
![]()
ЛАБОРАТОРНАЯ РАБОТА №3
Интегрирование рациональных выражений
Метод неопределенных коэффициентов
Так как из неправильной рациональной дроби можно выделить целую часть, интегрирование которой не представляет трудностей, то достаточно заняться интегрированием правильных дробей (у которых степень числителя ниже степени знаменателя).
Остановимся на так называемых простых дробях. Это дроби следующих четырех типов:
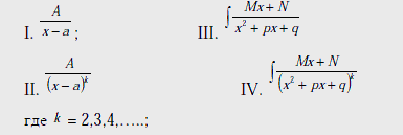
где ![]() = 2,3,4,…..;
= 2,3,4,…..;
![]() -вещественные числа.
-вещественные числа.
Рассмотрим интегралы от данных дробей ![]() I-IV:
I-IV:
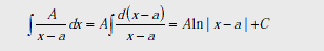

Для интегрирования дробей вида III,IV в трехчлене ![]() выделим полный квадрат:
выделим полный квадрат:
![]()
Делаем подстановку:
![]() и
и 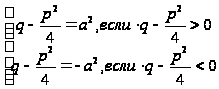
В случае III имеем:
Если
![]() , то
, то
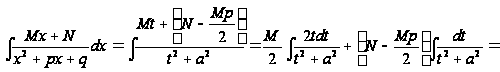
![]() .
.
Если
![]() , то
, то 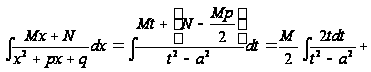
![]()
В случае IV будем иметь:
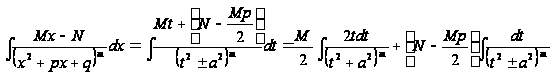
![]()
Первый интеграл вычисляется с помощью подстановки: ![]() ,
, ![]()
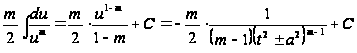 ,
,
а второй интеграл вычисляется с помощь![]() рекуррентной формулы. Пусть
рекуррентной формулы. Пусть
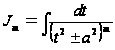 , где
, где ![]() =2,3,4…
=2,3,4…
Проинтегрируем интеграл ![]() по частям, положив
по частям, положив
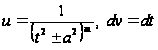 ,
, 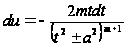
А затем, добавив и вычтя в числителе получившиеся под знаком интеграла функции и произведя деление так, как это указано ниже, получим

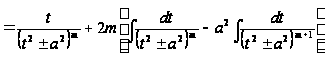 ,
,
то есть
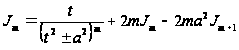
![]()
 ,
,
m=2,3,4…. (*)
Интервал ![]() легко вычисляется. Формула (*) позволяет вычислить
легко вычисляется. Формула (*) позволяет вычислить ![]() ; зная же
; зная же ![]() , по этой же формуле можно найти значение и
, по этой же формуле можно найти значение и ![]() , продолжая процесс дальше, можно найти и выражение для любого интеграла
, продолжая процесс дальше, можно найти и выражение для любого интеграла ![]() .
.
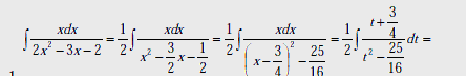
Пример1
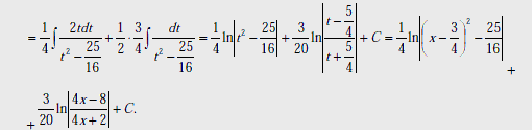
Пусть ![]() и
и ![]() - многочлены с действительными коэффициентами.
- многочлены с действительными коэффициентами.
Метод неопределенных коэффициентов состоит в следующем: для данной дроби ![]() пишется разложение:
пишется разложение:
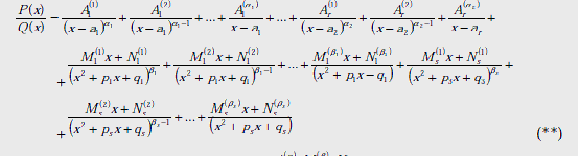
в котором коэффициенты ![]() считаются неизвестными (
считаются неизвестными ( ![]() ;
; ![]() ;
;![]()
![]() ). После этого равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты. При этом, если степень многочлена
). После этого равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты. При этом, если степень многочлена ![]() равна
равна ![]() , то, вообще говоря, в числителе правой части равенства (**) после приведения к общему знаменателю получается многочлен степени
, то, вообще говоря, в числителе правой части равенства (**) после приведения к общему знаменателю получается многочлен степени ![]() , т.е. многочлен с
, т.е. многочлен с ![]() коэффициентами; число же неизвестных
коэффициентами; число же неизвестных ![]() так же равняется
так же равняется ![]() :
: ![]() . Таким образом, мы получаем систему
. Таким образом, мы получаем систему ![]() уравнений с
уравнений с ![]() неизвестными.
неизвестными.
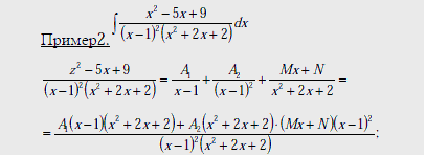
раскроем скобки, располагаем степени ![]() по убывающей, получаем:
по убывающей, получаем:
![]()
Сравниваем коэффициенты при одинаковых степенях ![]() :
:
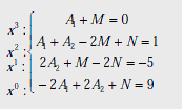
Решаем полученную систему, находим неизвестные коэффициенты:
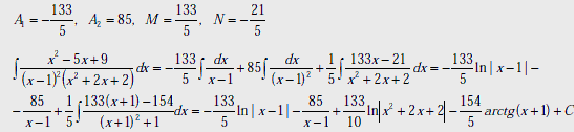
Варианты
Вычислить интегралы:
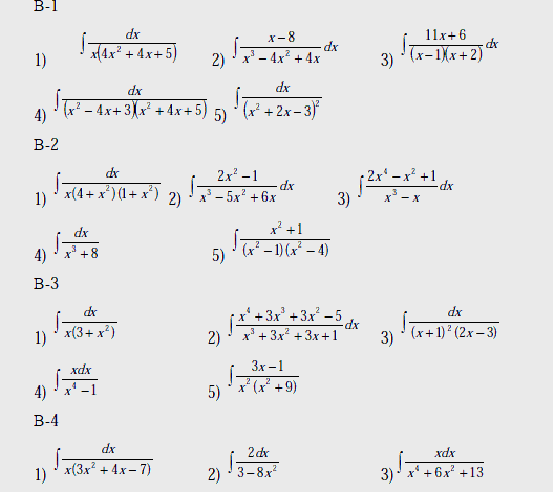

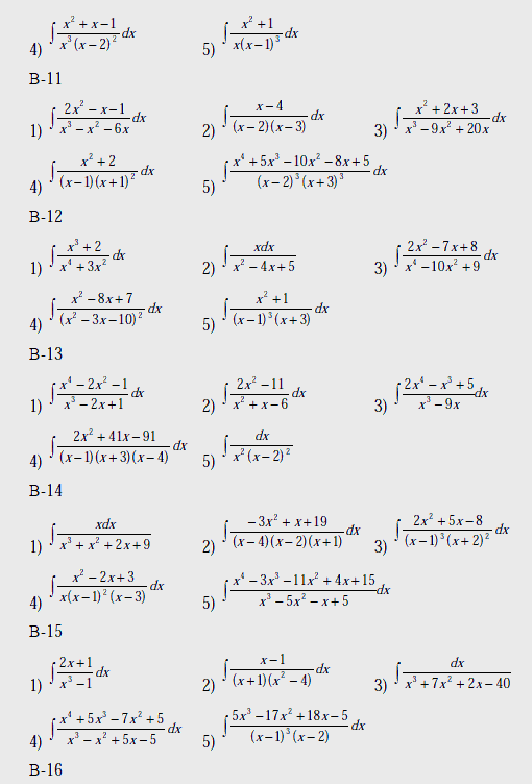


Вопросы к лабораторной работе №3
Приведите примеры интегралов, не выражающихся в конечном виде через элементарные функции.
В чем заключается характерная особенность класса рациональных функций?
Перечислить четыре типа простых дробей.
Покажите, как вычисляется интеграл вида ![]()
Покажите подробно, как вычисляется интеграл вида ![]() и какую при этом выгодно применить подстановку.
и какую при этом выгодно применить подстановку.
Покажите подробно, как вычисляется интеграл вида ![]() и какие подстановки следует при этом применять.
и какие подстановки следует при этом применять.
В чем состоит применение метода неопределенных коэффициентов к разложению правильной дроби в сумму простых?
8) С помощью каких функций выражается в конечном виде интеграл
от любой рациональной функции?
ЛАБОРАТОРНАЯ РАБОТА № 4
Интегрирование рациональных дробей. Метод Остроградского
Метод Остроградского позволяет чисто алгебраическим путем выделить рациональную часть интеграла.
Пусть имеем правильную дробь ![]() , которую будем предполагать несократимой, и пусть знаменатель ее Q разложен на простые множители
, которую будем предполагать несократимой, и пусть знаменатель ее Q разложен на простые множители
![]()
![]() (*)
(*)
Тогда интеграл от этой дроби представится в виде суммы интегралов от дробей вида:
![]() (1)
(1)
или
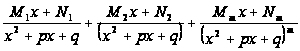 (2)
(2)
Если ![]() (или
(или ![]() ) больше единицы, то интегралы всех дробей группы (1) или (2) , кроме первой, преобразуются по формуле
) больше единицы, то интегралы всех дробей группы (1) или (2) , кроме первой, преобразуются по формуле
![]()
или
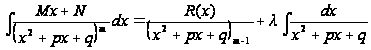
Объединяя все результаты, окончательно придем к формуле вида
![]() (3)
(3)
Рациональная часть интеграла ![]() , получена от сложения выделенных выше рациональных частей; следовательно, прежде всего она является правильной дробью, а ее знаменатель имеет разложение
, получена от сложения выделенных выше рациональных частей; следовательно, прежде всего она является правильной дробью, а ее знаменатель имеет разложение
![]()
Что касается дроби ![]() , оставшейся под знаком интеграла, то она получилась от сложение дробей вида I и II (Л. Р.№2), так что она тоже правильная и
, оставшейся под знаком интеграла, то она получилась от сложение дробей вида I и II (Л. Р.№2), так что она тоже правильная и ![]() . Очевидно , Q=
. Очевидно , Q=![]() (см.(*)).
(см.(*)).
(3)называется формулой Остроградского. Дифференцируя, можно представить ее в равносильной форме ![]()
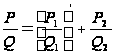 (4)
(4)
Так как производная ![]() содержит все простые множители, на которые разлагается, то
содержит все простые множители, на которые разлагается, то ![]() является наибольшим общим делителем
является наибольшим общим делителем ![]() и
и ![]() , так что
, так что ![]() может быть определено по этим многочленам (последовательным делением). Тогда
может быть определено по этим многочленам (последовательным делением). Тогда ![]() определяется простым делением
определяется простым делением ![]() на
на ![]() . Обратимся к определению числителей
. Обратимся к определению числителей ![]() и
и ![]() в формуле (4).
в формуле (4).
Для этого используем метод неопределенных коэффициентов.
Перепишем (4) в виде:
![]()
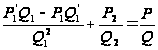 (5)
(5)
Покажем теперь, что первую дробь всегда можно привести к знаменателю ![]() , сохранив целым числитель. Именно,
, сохранив целым числитель. Именно,
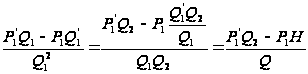 , (6)
, (6)
где ![]() означает частное
означает частное ![]() . Освобождаясь от общего знаменателя
. Освобождаясь от общего знаменателя ![]() , придем к тождеству двух многочленов (сравни (5) и (6)).
, придем к тождеству двух многочленов (сравни (5) и (6)).
Пример. 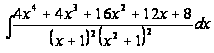
Имеем
![]()
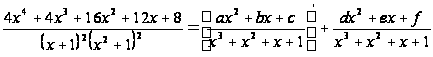 .
.
Откуда
![]()
Приравнивая коэффициенты при одинаковых степенях в обеих частях , получим:
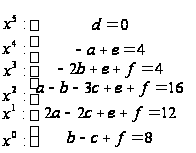
![]()
Таким образом,
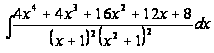 =-
=-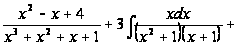
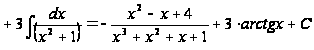
Варианты
Вычислить интегралы:
В-1
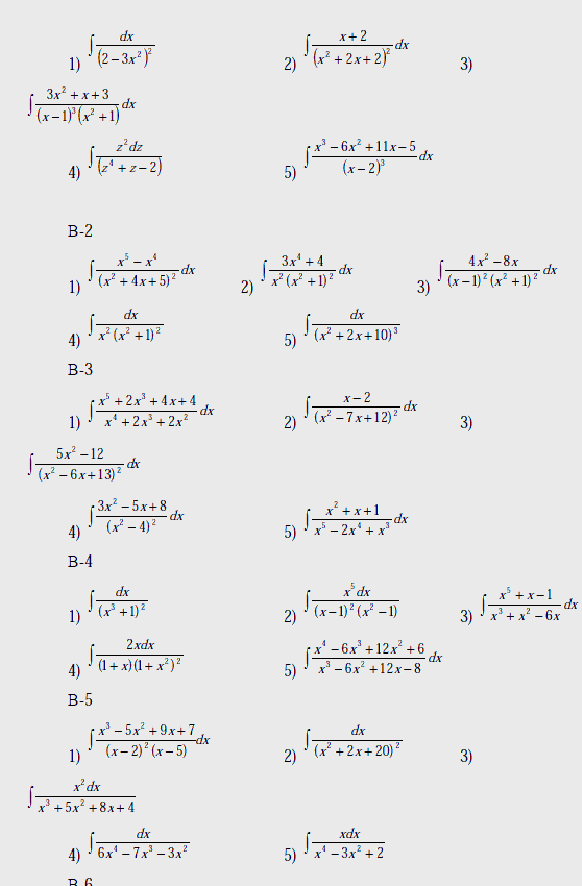
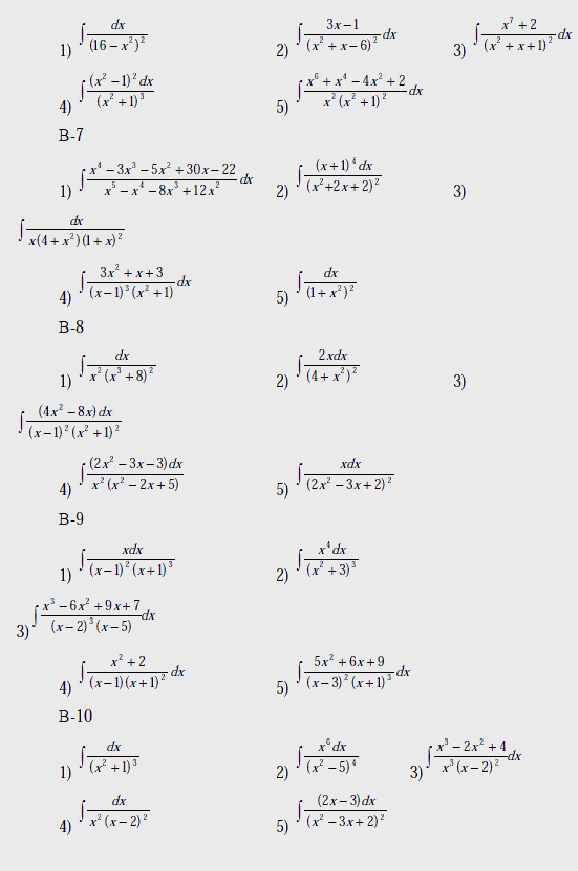

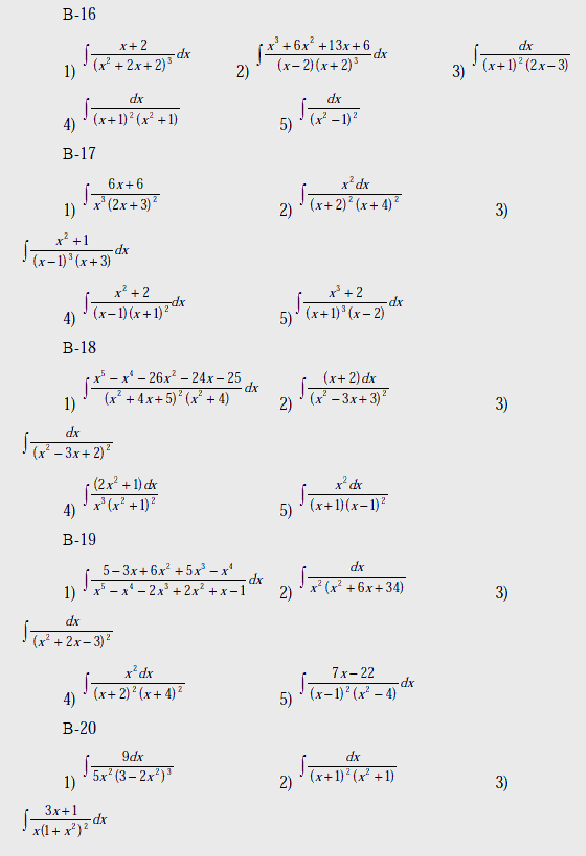
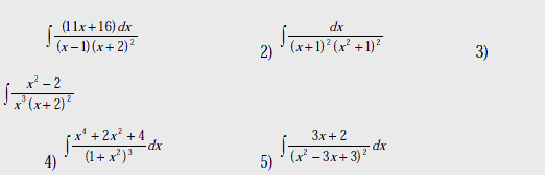
Вопрос к лабораторной работе №4
1. В чем заключается метод Остроградского и когда им пользуются?
ЛАБОРАТОРНАЯ РАБОТА №5
Интегрирование тригонометрических функций
Дифференциалы вида
![]() , (I)
, (I)
где ![]() - рациональная функция от двух переменных, могут быть приведены к более простому виду с помощью подстановки
- рациональная функция от двух переменных, могут быть приведены к более простому виду с помощью подстановки
![]() . (*)
. (*)
При этом используется формулы из тригонометрии:
 ;
; 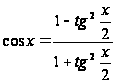 ;
;
Тогда:
![]() ;
; ![]() ;
; ![]() (**)
(**)
Подстановка (*) называется универсальной тригонометрической подстановкой.
Пример1. Вычислить интеграл ![]()
Решение: Сделаем подстановку ![]() , пользуясь (**), получим
, пользуясь (**), получим

=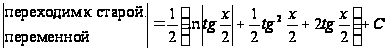
В некоторых случаях можно использовать более простые подстановки. Рассмотрим эти случаи.
Замечание 1: Если целая или дробная рациональная функция ![]() не меняет своего значения при изменении знака у одного из аргументов, например, т. е.
не меняет своего значения при изменении знака у одного из аргументов, например, т. е. ![]() , то она может быть приведена к виду
, то она может быть приведена к виду ![]() , содержащему лишь четные степени
, содержащему лишь четные степени ![]() .
.
Если же, наоборот, при изменении знака ![]() функция
функция ![]() так же меняет знак, т.е.
так же меняет знак, т.е. ![]() , то она проводится к виду
, то она проводится к виду ![]() .
.
Рассмотрим три случая:
1. Пусть теперь ![]() меняет знак при изменении знака
меняет знак при изменении знака ![]() , тогда
, тогда
![]()
и рационализация достигается подстановкой ![]() .
.
2. Аналогично, если ![]() меняет знак при изменении знака
меняет знак при изменении знака ![]() , то
, то
![]() ,
,
так что здесь целесообразна подстановка ![]() .
.
3. Предположим, наконец, что функция ![]() не меняет своего значения при одновременном изменении знаков
не меняет своего значения при одновременном изменении знаков ![]() и
и ![]() :
: ![]() . В этом случае, заменяя
. В этом случае, заменяя ![]() на
на ![]() будем иметь:
будем иметь: ![]() . По свойству функции R , если изменить знаки
. По свойству функции R , если изменить знаки ![]() и
и ![]() (отношение
(отношение ![]() при этом изменяется):
при этом изменяется):
![]() а тогда, как мы знаем
а тогда, как мы знаем ![]() .
.
Поэтому
![]()
=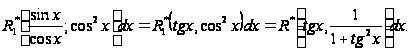
Поэтому здесь используется подстановка ![]() .
.
Замечание 2. Каково бы ни было рациональное выражение ![]() , его можно представить в виде суммы трех выражений рассмотренных типов:
, его можно представить в виде суммы трех выражений рассмотренных типов:
![]()
Первое из этих выражений меняет знак при изменении знака ![]() , второе меняет знак при изменении
, второе меняет знак при изменении ![]() , а третье сохраняет значение при одновременном изменении знаков
, а третье сохраняет значение при одновременном изменении знаков ![]() и
и ![]() . Разбив
. Разбив ![]() на соответствующие слагаемые, можно к первому из них применить подстановку
на соответствующие слагаемые, можно к первому из них применить подстановку ![]() , ко второму - подстановку
, ко второму - подстановку ![]() и, наконец, к третьему - подстановку
и, наконец, к третьему - подстановку ![]() . Таким образом, для вычисления
. Таким образом, для вычисления 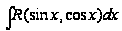
Подобные работы: