О теории вероятностей

Р(А+В)=Р(А)+Р(В).

Следствие1.

Если А₁,А₂, …, А_n- попарно несовместные события, то вероятность их суммы равна сумме вероятностей этих событий.

Следствие2.

Вероятность суммы попарно несовместных событий А₁,А₂, …, А_n, образующих полную группу, равна 1.

Следствие3.

События А и `А несовместны и образуют полную группу событий, поэтому

Р(А +`А) = Р(А) + Р(`А) = 1. Отсюда Р (`А) = 1 – Р(А).

Теорема2.

Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их произведения:

Р (А+В) = Р(А)+Р(В) – Р (А*В).

Два события А и В называются независимыми, если появление одного из них не влияет на вероятность появления другого (в противном случае события зависимы).

Теорема3.

Вероятность произведения двух независимых событий равна произведению их вероятностей Р(А*В)=Р(А)*Р(В).

Следствие.

Вероятность произведения n независимых событий А₁,А₂, …, А_n равна произведению их вероятностей.

Условной вероятностью события В при условии, что событие А уже произошло, называется число Р(АВ)/Р(А)=Р(В/А)Р_А(В).

Теорема4.

Вероятность произведения двух зависимых событий А и В равна произведению вероятности наступления события А на условную вероятность события В при условии что событие А уже произошло:

Р(А*В) =Р(А)*Р(В/А).

Следствие.

Если события А и В независимы, то из теоремы 4 следует теорема 3.

Событие В не зависит от события А, если Р(В/А) = Р(В). Теорему 4 можно обобщить на n событий.

Теорема5.

Вероятность произведения n зависимых событий А₁,А₂, …, А_nравна произведению последовательных условных вероятностей:

Р(А₁*А₂*…*А_n-1*A_n)= P(A₁)*P(A₂/A₁)*...*P(A_n/A₁*A₂*...*A_n-1).

Теорема6.

Вероятность наступления хотя бы одного из событий А₁,А₂, …, А_nравна разности между единицей и вероятностью произведении отрицаний событий А₁,А₂, …, А_n:

Р(А)=1-Р(`А<sub>1</sub>*`А₂*…*`А<sub>n</sub>)=1- P(`A₁)*P(`A<sub>2</sub>/`A₁)*...*P(`A<sub>n</sub>/`A₁*`A<sub>2</sub>*...*`A_n-1).

Следствие1.

Вероятность наступления хотя бы одного из событий А₁,А₂, …, А_nнезависимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:

Р(А)=1-Р(`А<sub>1</sub>)Р(`А₂)…Р(`А_n).

Следствие2.

Если события А₁,А₂, …, А_nнезависимы и имеют одинаковую вероятность появиться (Р(А₁)=Р(А₂)=…Р(А_n)= р, Р(А_i)= 1-р=q ), то вероятность появления хотя бы одного из них равна Р(А)=1-qⁿ .

5. Формулы полной вероятности и вероятности гипотез

Пусть событие А может наступать только одновременно с одним из попарно несовместных событий Н₁, Н₂, ..., Н_n, образующих полную группу. Тогда вероятность события А определятся по формуле полной вероятности:

Р(А) = Р(Н₁)*P(А/Н₁) + Р(Н₂)*Р(А/Н₂) +...+ Р(Н_n)*Р(А/Н_n), или Р(А)= Σ Р(Н_i)*Р(А/Н_i),

где события Н₁,Н₂, ...,Н_n, - гипотезы, a P(A/H_i) - условная вероятность наступления события А при наступлении i-ой гипотезы (i=1, 2,..., n).

Условная вероятность гипотезы Н_i при условии того, что событие А произошло, определяется по формуле вероятности гипотез или формуле Байеса (она позволяет пересмотреть вероятности гипотез после наступления события А):

Р(Н_i/А)=(P(H_i)*P(A/H_i))/P(A).

6. Формула Бернулли

Пусть некоторый опыт повторяется в неизменных условиях n раз, причём каждый раз может либо наступить (успех), либо не наступить (неудача) некоторое событие А, где Р(А) = р - вероятность успеха, Р(А)=1-р= q - вероятность неудачи. Тогда вероятность того, что в к случаях из n произойдёт событие А вычисляется по формуле Бернулли

P_n(K) = C^k_n-p^k-q^n-k.

Условия, приводящие к формуле Бернулли, называются схемой повторных независимых испытаний или схемой Бернулли. Так как вероятности Р_n(к) для раз личных значений к представляют собой слагаемые в разложении бинома Ньютона

(p+q)ⁿ=C⁰_n*p⁰*qⁿ+C¹_n*p¹*q^n-1+…+C^k_n*p^k*q^n-k+…+Cⁿ_n*pⁿ*q⁰,

то распределение вероятностей P_n(k), где 0≤k≤n, называется биноминальным.

Если в каждом из независимых испытаний вероятности наступления события А разные, то вероятность наступления события А к раз в n опытах определяется как коэффициент, при к-ой степени полинома

φ_n(Z)=Π(q_i+p_iZ)=a_nZⁿ+a_n-1Z^n-1+…+a₁Z₁+a₀, где φ_n(Z) - производящая функция.

Невероятнейшее число наступивших событий в схеме Бернулли - к_о (к₀ c К) определяется из следующего неравенства: np-q≤k₀≤np+p.

7. Локальная формула Муавра-Лапласа

Если npq>10 , то

где вероятность р отлична от 0 и 1 (р→0,5), х =(k-np)/√npq.

Для облегчения вычислений функция

представлена в виде таблицы (прил.1).

φ(х) - функция вероятности нормального распределения (рис. 6) имеет следующие свойства:

1) φ(х)-четная;

2) точки перегиба х = ± 1;

3) при х≥5, φ(х)→0, поэтому функция φ(х) представлена в виде таблицы для 0≤х≤5 (прил.1).

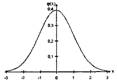
Рис. Функция вероятности нормального распределения

8. Интегральная теорема Муавра-Лапласа.

При больших значениях n , для вычисления вероятности того, что произойдет от к₁, до к₂ событий по схеме

Бернулли, используется интегральная формула Муавра-Лапласа

P_n(k₁≤k≤k₂)=Ф(x₂)- Ф(x₁),

где x₁=(k₁-np) /(√npq), x₂=(k₂-np)/(√npq), Ф(x) – функция Лапласа. (рис.7)

Ф(х) имеет следующие свойства:

1. Ф(-х)= -Ф(х) - функция нечетная, поэтому достаточно изучать её для неотрицательных значений х

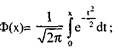
2. Функция Ф(х) возрастает на всей числовой оси;

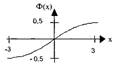
Рис. Функция Лапласа

3. При х≥5, Ф(х)→1/2 (y = 0,5 горизонтальная асимптота при х>0), поэтому функция представлена в виде таблицы Для 0≤х≤5 (прил.1).

4. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях не более чем на некоторое число ε>0

9. Формула Пуассона

Если npq<10 и р<0,1, то

где λ=np.

10. Случайные величины и их виды

Случайной величиной (СВ) называют такую величину, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать какое именно значение она примет. (Более точно, СВ - это действительная функция, определенная на пространстве элементарных событий Q). Случайные величины обозначаются последними буквами латинского алфавита - X,Y,Z. Случайные величины могут быть трех типов: - дискретные, - непрерывные, - смешанные (дискретно-непрерывные). Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений. Непрерывная случайная величина (НСВ) в отличие от ДСВ принимает бесконечное несчетное число значений. Например мишень имеет форму круга радиуса R. По этой мишени произвели выстрел с обязательным попаданием. Обозначим через Y расстояние от центра мишени до точки попадания, Ye (0; R). Y - непрерывная случайная величина, так как она принимает бесконечное несчетное число значений.

Пусть X - дискретная случайная величина, которая принимает значения х₁, х₂, ...,х_n,... с некоторой вероятностью р_i, где i = 1, 2, ..., n,... Тогда можно говорить о вероятности того, что случайная величина X приняла значение х_i: р_i=Р(Х=х_i).

ДСВ может также представляться в виде многоугольника распределения – фигуры, состоящей из точек, соединенных отрезками. Над СВ устанавливаются операции сложения и умножения.

Суммой двух СВ X и Y наз-ся случайная величина, которая получается в рез-те сложения всех значений случайной величины X и всех значений СВ Y, соответствующие вероятности перемножаются. Произведением двух СВ X и Y наз-ся СВ, которая получается в рез-те перемножения всех значений СВ X и всех значений СВ Y, соответствующие вероятности перемножаются.

11. Математическое ожидание

Математическим ожиданием М(Х) ДСВ X называется среднее значение случайной величины:

Или иначе, М(Х) - это сумма парных произведений случайной величины на соответствующую вероятность:

Мода М_о(Х) распределения - это значение СВ, имеющее наиболее вероятное значение.

Медиана М_е(Х) - это значение случайной величины, которое делит таблицу распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5. Медиана обычно не определяется для ДСВ.

Свойства математического ожидания:

1) М(С)=С, где С=const;

2)М(СХ) = СМ(Х);

3) M(X±Y) = М(Х) ± M(Y);

4) Если случайные величины X и Y, независимы, то M(XY) = M(X)*M(Y).

Для биномиального распределения М(Х)=nр;

для геометрического распределения М(Х)= 1/р;

для распределения Пуассона М(Х)=λ;

для гипергеометрического распределения М(Х) = n(M/N).

12. Дисперсия ДСВ и ее свойства

Математическое ожидание квадрата отклонения СВ от ее математического ожидания:

D(X) = M(x-M(X)²) = =(х₁-М(Х))²р₁+(х₂-М(Х))²р₂+....+(x_n-М(Х))²р_n .(2.3.2)

Свойства дисперсии:

1) D(С) = 0, где С=соnst;

2) D(CX)=C²D(X);

3) D(X)=M(X²)-(M(X))², где М(Х²) = х²₁ р₁ + x²₂ p₂ + ...+ х²_n р_n;

4) Если СВ X и Y независимы, то D(X±Y)=D(X) + D(Y);

5) D(OX)=D(X);

6) Для любых СВ X и Y, D(X±Y)=D(X)+D(Y)±2cov(X,Y), где cov(X,Y)=M((X-m_x)(Y-m )) - ковариация случайных величин X и Y (М(Х)= m_x, M(Y)= m).

Дисперсия характеризует средний квадрат отклонения ДСВ, поэтому на практике часто используют в качестве характеристики разброса среднее квадратическое отклонение σ(Х)= √D(X) , которое имеет ту же размерность, что и СВ X.

Для биноминального закона

D(X)=npq, σ(X)=√npq;

для геометрического закона D(X)= q/p²;

для гипергеометрического D(X)=n(M/N)(1-M/N)(N-n)/(N-1);

для распределения Пуассона D(X)=λ.

Только для распределения Пуассона M(X)=D(X)= λ.

13. Показательное распределение.

НСВ X, принимающая неотрицательные значения, имеет показательное распределение, если ее дифференциальная функция имеет вид

где Я =const, Я >0.

Интегральная функция показательного закона с параметром λ:

Рис. Показательный закон

Если СВ X распределена по показательному закону, то:

1. Математическое ожидание М(Х) = 1/λ ;

2. Дисперсия D(X)=1/λ², среднее квадратическое отклонение

σ(X)=√D=1/λ.

3. Вероятность попадания СВ X в заданный интервал определяется по формуле

Р(а≤х-λа-е^-λb.

Замечание. Показательное распределение играет большую роль в теории массового обслуживания (ТМО), теории надежности. В ТМО параметр X - среднее число событий, приходящихся на единицу времени. При определенных условиях число событий, произошедших за промежуток времени т, распределено по закону Пуассона с математическим ожиданием а =λτ. Длина промежутка t, между произвольными двумя соседними событиями, подчиняется показательному закону: P(Tλt.

14. Закон распределения дискретной случайной величины

1. Биномиальный закон распределения. Случайная величина X принимает значения 0, 1, 2, 3, 4, 5,...,n, с вероятностью, определяемой по формуле Бернулли:

2. Закон распределения Пуассона. Случайная величина X принимает бесконечное счетное число значений: 0, 1, 2, 3, 4, 5,..., к,... , с вероятностью, определяющейся по формуле Пуассона:

где Х>0 - параметр распределения Пуассона.

При n→∞ и р→0 биномиальный закон приближается к закону распределения Пуассона, где λ, = np.

Геометрический закон распределения. Пусть Р(А)=р - вероятность наступления события А в каждом опыте, соответственно, q=l-p - вероятность не наступления события А.

Вероятность наступления события А в к-ом опыте определяется по формуле:

P(X=k)=p-q^k-1. (2.2.2.)

Случайная величина X, распределенная по геометрическому закону принимает значения 1, 2,...,к,... , с вероятностью, определяемой по формуле (2.2.2):

4. Гипергеометрический закон распределения. Пусть в урне N-шаров, из них М белых, а остальные (N - М) черные. Найдем вероятность того, что из извлеченных n шаров m белых и (n-m) черных.

N= М + (N-M); n = m + (n-m);

С^m_M - число способов выбора m белых шаров из М;

С^n-m_N-M- число способов выбора (n-m) черных шаров из (N-M).

По правилу произведения, число всех возможных наборов из m белых и (n-m) черных равно С^m_M С^n-m_N-M;

Cⁿ_N- общее число способов выбора из N шаров n.

Отсюда, по формуле классического определения вероятности, P(A)= (С^m_M С^n-m_N-M)/ Cⁿ_N

Ограничения на параметры: М≤N, m≤n; m = m₀, m₀ +1, m₀+2,..., min(M,n), где m₀=max{0, n-(N-M)}. Случайная величина Х, распределенная по гипергеометрическому закону распределения (при т=0,1,2,3,...,М), имеет вид:

Гипергеометрический закон определяется тремя параметрами N, М, n. При n<0,1N этот закон стремится к биномиальному.

Замечание.

1. В теории вероятностей различают две основные схемы: выбора элементов с возвращением каждый раз обратно и выбора без возвращения, которые описываются соответственно биномиальным и гипергеометрическим законами.

2. Геометрический закон описывает схему повторения опытов (в каждом из которых может наступить или не наступить событие А: Р(А)=р, q=l-p), до первого появления события А, то есть фактически это отрицательное биномиальное распределение при m=1.

16. Одинаково распределённые, взаимонезависимые дискретные случайные величины

СВ называют одинаково распределенными, если они имеют одинаковые законы распределения. Поэтому у них совпадают числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.

Пусть X₁, Х₂,..., Х_n одинаково распределенные, взаимонезависимые ДСВ, тогда:

M(X₁) = М(Х₂) = ... = М(Х_n) = М(Х), D(X₁) = D(X₂) = ...= D(X_n)=D(X).

Рассмотрим характеристики их средней арифметической X = (X₁+X₂+…+X_n)/n:

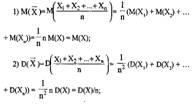
-стандартное отклонение СВ X.

Дисперсия относительной частоты (m/n) появления события А в n независимых испытаниях (в каждом из которых событие А появляется с вероятностью равной р, и не появляется с вероятностью q= 1-р; m-число появлений события А в серии из n испытаний), определяется по формуле

15. Дифференциальная функция распределения и ее свойства

СВ X непрерывна, если ее интегральная функция непрерывна на всей числовой оси. СВ X непрерывна и имеет дифференциальную функцию, если ее интегральная функция непрерывна и дифференцируема всюду, за исключением конечного числа точек на любом конечном промежутке.

Дифференциальной функцией (функцией плотности вероятности) СВ X называется производная ее функции распределения: f(x)=F'(x).

С помощью дифференциальной функции можно получить формулу вероятности попадания СВ X в заданный интервал:

Свойства дифференциальной функции:

). f(x)≥0;

16. Числовые характеристики непрерывных случайных величин

1) Математическое ожидание НСВ X определяется по формуле

М(Х)= ∫xf(x)dx.       (2.7.1)

Если НСВ X определена на интервале (а; b), то

М(Х)= ∫xf(x)dx.

2) Мода НСВ X будет определяться как максимум ее дифференциальной функции: М_о(Х) = max f (x).

3) Медиана определяется как значение случайной величины, которое делит площадь под дифференциальной функцией на две равные части. M_e(X): P(xe(X))=P(x>M_e(X))=1/2.

4). Дисперсия НВС

Все св-ва дисперсии и мат-го ожидания, установленные для ДСВ, сохраняется для НСВ.

Замечание. Если распределение симметрично, то его мода, медиана и математическое ожидание совпадают.

5). Моменты случайных величин.

Кроме характеристик положения и рассеяния существует ряд других числовых характеристик распределения, например, моменты.

Начальным моментом порядка s называется математическое ожидание степени s CB X: α_s=M(X^s).

Для ДСВ:

При s=l:α₁, = M(X) = m_x, то есть, первый начальный момент - это математическое ожидание СВ.

Отклонение СВ от ее математического ожидания называется центрированной СВ X: X = Х-m_х.

Центральным моментом порядка s СВ X называется математическое ожидание степени s, соответствующей центрированной СВ: μ_s=μ(X^s)=M((x-M(X))^s).

При вычислении центральных моментов пользуются формулами связи между центральными и начальными моментами:

μ₁=0,

μ₂=α₂-m²_x,

μ₃=α₃-3m_xα₂+2m³_x,

μ₄=α₄-4m_xα₃+6m²_xα₂-3m⁴_x.

Обычно рассматривают первые четыре центральных момента:

1). μ₁=M(x-m_x)=0 – мат-ое ожидание центрированной СВ равно нулю;

2). μ₂= M(x-m_x)²=D(X) – второй центральный момент – это дисперсия;

3). μ₃= M(x-m_x)³- третий центральный момент может служить для характеристики асимметрии, обычно рассматривают безразмерный коэффициент асимметрии

Sk=μ₃/σ³.

4). Четвёртый центральный момент

μ₄=M(x-m_x)⁴,

может служить для характеристики “крутости” или островершинности распределения, описывающиеся с помощью эксцесса:

E_x=(μ₄/σ⁴)-3.

Основным моментом порядка s называется нормированный центральный момент порядка s:

r_s= μ_s/σ^s, то есть Sk=r₃, Ex=r₄-3

17. Равномерный закон распределения

СВ X распределена по равномерному (прямоугольному) закону, если все значения СВ лежат внутри некоторого интервала и все они равновероятны (точнее обладают одной плотностью вероятности).Например, если весы имеют точность 1г и полученное значение округляется до ближайшего целого числа k, то точный вес можно считать равномерно распределенной СВ на интервале (k-0,5; k+0,5).

Дифференциальная функция равномерного закона на интервале (α,β) (рис. 11):

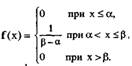
Интегральная функция равномерного закона на интервале (α,β) (рис. 11):

Рис. Дифференциальная функция

2). Интегральная функция.

Основные числовые характеристики равномерного закона:

1. Математическое ожидание

М(Х) совпадает, в силу симметрии распределения, с медианой.

Моды равномерное распределение не имеет.

Дисперсия

Отсюда, среднее квадратическое отклонение

Третий центральный момент

поэтому распределение симметрично относительно М(Х).

Четвёртый центральный момент

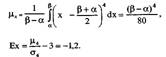
Вероятность попадания СВ в заданный интервал (а;b). Пусть СВ X распределена по равномерному закону,

18. Закон больших чисел

Под законом больших чисел в теории вероятностей понимают совокупность теорем, в которых утверждается, что существует связь между средним арифметическим достаточно большого числа случайных величин и средним арифметическим их математических ожиданий.

В1927 г. Гейзенберг открыл принцип неопределенности, который утверждает, что измерительное познание ограничено. Неопределенность является неотъемлемой частью нашей жизни, однако, при большом числе однотипных опытов можно установить определенные закономерности.

19. Нормальный закон распределения

Нормальный закон распределения играет исключительную роль в теории вероятностей. Это наиболее часто встречающийся закон распределения, главной особенностью которого является то, что он является предельным законом, к которому, при определённых условиях, приближаются другие законы распределения.

Дифференциальная функция нормального закона имеет вид

Числовые характеристики нормального закона:

1. Математическое ожидание характеризует центр распределения

где e^x=exp(x);

2. Дисперсия характеризует форму распределения

Свойства дифференциальной функции нормального закона:

1. Область определения: D_f = R;

2. Ось ОХ - горизонтальная асимптота;

3. х = а±σ - две точки перегиба;

4. Максимум в точке с координатами (а; 1/(σ√2π);

5. График симметричен относительно прямой х=а;

6. Моменты:

μ₁=μ₃=…=μ_2k+1=…=0,

μ₂=σ², μ₄=3σ⁴,

Sk=μ³/σ³=0, Ex=μ⁴/σ⁴-3=0

7. Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется, по свойству интегральной функции

где

интегральная функция нормального закона (рис.14); Ф(х)- функция Лапласа.

Свойства интегральной функции нормального закона:

1. Ф* (-∞)=0;

2. Ф*(+)=1;

3. Ф*(x)=1/2+Ф(x);

4. Ф*(-x)=1-Ф*(x).

Вероятность заданного отклонения. Правило трех сигм.

Найдем вероятность того, что случайная величина X, распределённая по нормальному закону, отклонится от математического ожидания М(Х)=а не более чем на величину ε>0.

Р(|х-а|<ε)= Р(-ε< х-а<+ε) = Р(а-ε<х< а+е) =Ф^*((a+ε-a)/σ)-Ф^*((a-ε-a)/σ)=Ф^*(ε/σ)-(1-Ф^* (ε/σ))=2Ф^* (ε/σ)-1.

Или, используя функцию Лапласа:

P(|X-a|<ε)=2Ф(ε/σ).

Найдём вероятность того, что нормально распределённая СВ X отклонится от M(X)=a на σ, 2σ, 3σ:

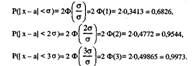
Отсюда следует правило Зσ. если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратическое отклонение (Зσ).

20. Многомерные случайные величины

В практических задачах приходится сталкиваться со случаями, когда результат описывается двумя и более случайными величинами, образующими систему случайных величин (случайный вектор). Например, точка попадания снаряда имеет две координаты: х и у, которые можно принять за систему случайных величин, определенных на одном и том же пространстве элементарных событий Ω.

Закон распределения дискретной двумерной случайной величины можно представить в виде таблицы, характеризующей собой совокупность всех значений случайных величин и соответствующих вероятностей:

В общем случае двумерная случайная величина задается в виде интегральной функции, которая означает вероятность попадания двумерной случайной величины в квадрант левее и ниже точки с координатами (х, y):

F(x, у) = Р(Х<х, Y

21. Свойства интегральной функции:

1. F - не убывает и непрерывна слева по каждому аргументу.

2. F(-∞, у)= F(x,-∞)= F(-∞, -∞)= 0.

3. F(+∞, у)= F₂(y) - функция распределения случайной величины Y. F(x,+∞)= F₁,(x) - функция распределения случайной величины X.

4. F(+∞,+∞)=l.

Вероятность попадания двумерной случайной величины в прямоугольник определяется исходя из определения интегральной функции двумерной случайной величины:

Р((х, у) c D) = F(β,δ) - F(α,β) - F(β,γ) + F(α,γ).

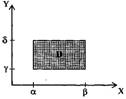
Рис. Вероятность попадания точки (х, у) в прямоугольник D

Случайные величины X, Y независимы, если

F(x, у) = = F₁(x)* F₂(y).

Дифференциальная функция системы двух непрерывных случайных величин определяется как вторая смешанная производная функции распределения:

f(x,y)=(∂²F(x,y))/∂x∂y=F″_xy(x,y).

Свойства дифференциальной функции:

l.f(x,y)>0;

Геометрически свойство 2 означает, что объем тела, ограниченного поверхностью f (x, у) и плоскостью XOY, равен 1.

Если случайные величины X и Y независимы, то

f(x,y) = f₁(x) f₂(y), где f₁(x)=F’₁(x),f₂(y)=F’₂(y).

В противном случае

f ( x , у ) = f₁( x ) f ( y / x )

или f ( x, y) = f₂( y ) f (x / y ),

где f(y/x)=f(x,y)/f₁(x) - условная дифференциальная функция CB Y при заданном значении

X = x, f(y/x)=f(x,y)/f₂(x) - условная дифференциальная функция СВ X при заданном значении Y= у;

- дифференциальные функции отдельных случайных величин X и Y, входящих в систему.

22. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции

Начальным моментом порядка s,h системы двух случайных величин X, Y называется математическое ожидание произведения степени s случайной величины X и степени h случайной величины Y:

α_s,h=M(X^sY^h)

Центральным, моментом порядка s, h системы СВ (X, Y) называется математическое ожидание произведения степеней s, h соответствующих центрированных случайных величин:

μ_s,h =M(X^SY^h), где X =X-М(X),

Y=Y-М(Y)

-центрированные случайные величины X и Y.

Основным моментом порядка s, h системы СВ (X,Y) называется нормированный центральный момент порядка s, h:

Начальные моменты α_1.0, α_0,1

α_1.0=M(X¹Y⁰)=M(X); α_0.1=M(X⁰Y¹)=M(Y).

Вторые центральные моменты:

μ_2,0=M(X²Y⁰)=M(x-M(X))²=D(X)

- характеризует рассеяние случайных величин в направлении оси ОХ.

μ_2,0 = M(X⁰Y²) = M(y-M(Y))² = D(Y)

- характеризует рассеяние случайных величин в направлении оси OY.

Особую роль в качестве характеристики совместной вариации случайных величин X и Y играет второй смешанный центральный момент, который называется корреляционным моментом - K(X,Y) или ковариацией –

cov(X,Y): μ_1,1=K(X,Y)=cov(X,Y)=M(X¹Y¹)=M(XY)-M(X)M(Y).

Корреляционный момент является мерой связи случайных величин.

Если случайные величины X и Y независимы, то математическое ожидание равно произведению их математических ожиданий:

М (XY)= М (X) М (Y), отсюда cov(X,Y)=0

Если ковариация случайных величин не равна нулю, то говорят, что случайные величины коррелированны. Ковариация может принимать значения на всей числовой оси, поэтому в качестве меры связи используют основной момент порядка s=1, h=1 ,который называют коэффициентом корреляции:

Свойства коэффициента корреляции:

1. -1ху<1.

2. Если r = +1, то случайные величины линейно зависимы;

3. Если r_ху = 0, то случайные величины некоррелированны, что не означает их