Physical Methods of Speed-Independent Module Design
Oleg Izosimov
INTEC Ltd, Room 321, 7a Myagi Street, Samara 443093, Russia
1. Introduction
Any method of logic circuit design is based on using formal models of gates and wires. The simplest model of a gate is determined by only two "parameters": (a) Boolean function is to be calculated, (b) fixed propagation delay. The simplest model of a wire is an ideal medium with zero resistance and consequently, with zero delay. Such simple models allow circuit design procedures which are a sequence of elementary steps easily realized by a computer.
When logic circuits designed by using the simplest models expose unreliable operation as in the case of gate delay variations, designers introduce less convenient but more realistic models with arbitrary but finite delay. Using more complicated models may produce logic circuits that are called speed-independent (1).
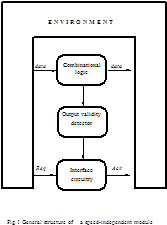
In speed-independent circuits transition duration can be arbitrary. So a centralized clock cannot be used. Instead special circuitry to detect output validity is applied. Besides, additional interface circuitry is needed to communicate with the environment in a handshaking manner. A speed-independent circuit can be seen as a module consisting of combinational logic (CL) proper, CL output validity detector (OVD) and interface circuitry (Fig.1). To enable OVD to distinguish valid output data from invalid ones, the redundant coding scheme was proposed (2). The main idea of the scheme is to enumerate all possible input and output data, both valid and invalid. The OVD must be provided with appropriate information on data validity. To realize the idea of redundant coding some constraints on CL design are imposed (3):
(i) CL must be free of delay hazards, i.e. CL output data word must not be dependent on the relative delay of signal paths through CL.
(ii) In changing between input states, any intermediate or transient states that are passed through must not be mapped by CL onto valid output states.
When these constraints were formulated, the circuit designers realised that not every Boolean description could be implemented in a speed-independent style. Other approaches to speed-independent module design were needed.
SIM design as a science has two branches: logical and physical. For a long time physical branch was overshadowed in spite of its competitiveness. The main properties of physical approach to SIM design are:
(a) Arbitrary coding scheme.
(b) Conventional procedure of operational unit design.
(c) Races of signals in SIM do not affect on its proper operation.
In this paper we propose an approach based on the physical nature of transitions in CL. We believe that each transition is actually a transfer of energy which can be naturally detected by physical methods.
From the viewpoint of a radio engineer CL behaves like a radio transmitter. It emits radio frequencies in the 108-1010Hz band modulated by signals of 106-108Hz. Obviously, the carrier wave is produced by gate switchings during transitions in CL. The modulating wave is produced by control schemes (OVD and interface circuitry) that detect transition completion and inform the environment about the readiness of CL. OVD is a kind of radio receiver that extracts the modulation envelope and enhances the received signal. The main properties that OVD circuit must expose from a radio engineer's point of view are selectivity and high gain. Since the useful signals can propagate through non-conducting medium, OVD circuits can be coupled with CL indirectly.
Advances in semiconductor technology gave birth to two methods of transition detecting based on two kinds of the information carrying signal, namely electromagnetic radiation and current consumption. Frequency of the signal produced by switching logic gates is determined by gate delay.
For instance, CMOS network of 1-ns gates produces 1-GHz signal, ECL array of 100-ps gates gives 10-GHz radiation. Logic circuits consisting of 10-ps gates will emit infra-red radiation. That signal could be easily detected by photosensitive devices.
2. Background
Let us have a closer look at the structure of speed-independent modules (SIM) as presented in Fig.1. All input data are processed in CL, all output data are obtained from CL, too. So, CL is the only unit in SIM which is involved in proper data processing. The result of that processing is specified by Boolean functions. Algorithms for calculating the Boolean function are realised by the internal structure of CL. Generally, its structure is series-parallel as well as algorithm implemented.
When -bit data word is put into the CL, or more signal propagation paths (SPPs) can be activated concurrently. So, one can say that the calculation of a Boolean function by CL is of parallel nature. On the other hand, each SPP is a gate chain which processes data in a serial manner. So, calculation in CL is also of sequential nature.
The OVD circuit is intended for detecting transient and steady "states" of CL. If any SPP in CL is still "active", CL is in transient state, otherwise it is in steady state. Each gate switching results in both logical and electromagnetic effects on its surrounding medium. The logical effects of switching has been heavily investigated; we consider physical one.
To provide speed-independence of the module the OVD and interface circuitry must also work in a speed-independent mode. This means that any arbitrary but finite transistor or wire delay cannot impair proper operation of OVD and interface circuitry.
The interface circuitry is a mediator between OVD and environment of SIM. It implements any kind of signalling convention, commonly a two- or four-cycle one (4) based on request Req and acknowledgement Ack signal using. The interface circuitry receives the output validity (OV) signal from the OVD circuit, a Req signal from the environment and transmits an Ack signal to the environment (Fig.1).
Consider an algorithm of operation for interface circuitry realizing speed-independent four-cycle signalling convention (FCSC). In accordance with FCSC the control signals must go in the following sequence: Req+OV-Ack+Req-Ack- where "+" corresponds to rising the signal and "-" corresponds to falling the signal. All signals are assumed to adhere to positive logic. Initially the signals Req and Ack are low, the signal OV is high. If the environment state changes, the Req signal rises and transient state of CL occurs (OV-). Upon completion of the transitions in CL, signal OV rises and the interface circuitry generates the Ack signal rising. After that the environment produces a falling Req signal and then the interface circuitry transmits the falling Ack signal to the environment. All the signals have to be reset into the initial state.
To develop the interface circuitry a circuit designer must take into account that any OVD circuit has finite (non-zero) turn-on delay ton. This means that OVD cannot respond on transitions of short duration t tr< ton .
An example of interface circuitry is shown in Fig.2. It contains a flip-flop, a NOR-gate, an asymmetrical delay and an inverter as an output stage (5).
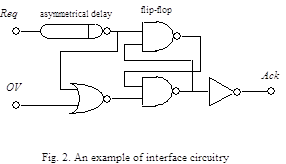
The asymmetrical delay is intended for delaying Req rising signal for + period where + > ton . Delaying Req falling signal noted - is to be as short as possible. Note that speed-independent operation of interface circuitry is vulnerable to delay + variation. If + becomes less than ton , proper operation of SIM can not be guaranteed. Otherwise, if + is much more than ton , performance of SIM will be significantly reduced. To provide exact accordance of + and ton a circuit emulator can be used.
Such an emulator is either an exact copy of OVD or its functional copy, i.e. resistive-capacitive model of OVD's critical path. In the chip the emulator must be placed next to active OVD circuit in order to ensure identical conditions of fabrication and operation.
In this example we use a simplified asymmetrical delay implemented as an asymmetrical CMOS inverter chain (Fig.3). Contrary to the common inverter an asymmetrical one has non-equal rise and fall times of output signal.
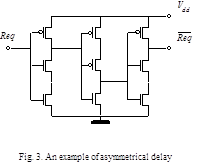
A time diagram for interface circuitry is presented in Fig.4 for two cases: (a) ttr< ton and (b) ttrton. In case (a) the signal sequence Req+Ack+ is formed for (++tNOR) period where tNOR is a NOR-gate delay. In case (b) the above sequence is formed for (ttr +toff+tNOR) duration where toff is a turn-off delay of OVD circuit. When the SIM returns to the initial steady state, the signal sequence Req-Ack- is formed for (-+tNOR) interval.

After considering the SIM in operation it is obvious that the main problems of the module design are in the area of CL and OVD interaction. This includes (a) kind of signal used as a carrier of information about CL output validity, and (b) method of OVD circuit design.
4. Current consumption detection
Using current consumption of CMOS CL for output validity detection was proposed in 1990 (7). Contrary to the method of EMR detection this one is based on introducing direct coupling of source and receiver. While CL is in steady state it consumes current of about 10-9-10-8A which does not allow OVD switching. The interface circuitry gets information on CL output validity and in turn informs the environment about CL readiness to input data processing. When an input data arrives CL changes its state to "transient", current consumption increases to 10-4-10-2A, which switches the OVD, thus informing the interface circuitry about output invalidity. The latter lets the environment know about CL business.
After the computations in the CL are finished, the current consumption decreases down to the steady state value, and the OVD sends a signal of output validity.
4.1 Information carrying signal
Current consumption by CMOS CL contains useful information on CL state. CMOS CL is a network of CMOS gates, so the current consumed by CL is a superposition of currents consumed by CMOS gates included in the CL. Each CMOS gate contains PMOS transistor and NMOS transistor networks (Fig.5). While a gate is in a steady state either the PMOS or the NMOS network is in a conducting mode. When a gate switches the non-conducting transistor network becomes conducting. There is usually a short period in switching time when both networks are in a conducting mode.

Generally, current consumed by a CMOS gate includes three components (9,10):
(a) leakage current Ilk passing between power supply and ground due to finite resistance of non-conducting transistor network;
(b) short-circuit current Isc flowing while both networks are in a conducting mode;
(c) load capacitance CL charge current ILC flowing while a CMOS gate is switching from low to high output voltage via conducting PMOS network and CL .
SPICE simulation has shown (5) that amplitude of current consumed by a typical CMOS inverter depends on CL and is limited by the non-zero resistance of the conducting PMOS network (Fig.7). The integral of consumed current is proportional to CL . When a gate switches from high to low output voltage, the component ILC is negative by direction and negligible by value (Fig.7b). It is evident, the switchings from high to low output voltage occur at the expense of energy accumulated in CL during the previous switching from low to high output voltage. The component Isc does not depend on direction in which a gate switches.

The component ILC equals to ILC = CLVddf where Vdd is a power supply voltage, f is a gate switching frequency. Veendrick has investigated the component Isc dependencies on CL and rise-fall time of input potential signal (10). He showed that if both input and output signal have the same rise-fall time, the component Isc cannot be more than 20 percent of summary current consumption (10). However, when the output signal rise-fall time is less than input one, the component Isc can be of the same order of magnitude as ILC. In that case it must be taken into account. As to the component Ilk, it entirely depends on CMOS process parameters and for state of the art CMOS devices Ilk is about 10-15 -10-12 A.
So, the analysis of CMOS gate current consumption allows us to conclude that in transient state a CMOS gate consumes a current I= Ilk+Isc+ILC and in steady state it consumes only Ilk<< I . The difference between two states from the viewpoint of current consumption is several orders of magnitude. So, CMOS gate output validity detection is possible, both in principle and in practice.
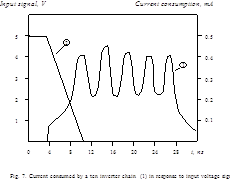
In Section 2 we presented series-parallel model of computations in CL. We showed that in every moment during switching current consumed by CL is a superposition of the currents consumed on the activated signal propagation paths (SPPs). Now, considering CL implemented by CMOS devices we should note that while logical signal propagates through SPP the neighbouring gates switch in opposite directions. That is why a curve of current consumed by a ten inverter chain (Fig.8) looks like a combination of crests and troughs. Nevertheless, in the very lowest point of the curve the current consumed by CL in a transient state remains several orders more than in a steady state.
4.2 OVD implementation
The proposed OVD circuit, shown in Fig.9, is a threshold circuit translating an analog current signal I into a logical signal OV.
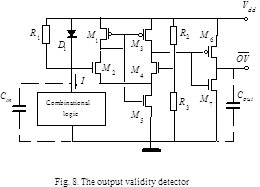
The OVD circuit contains a current-to-voltage converter (CVC) consisting of the resistor R1 and the diode D1. The OVD also contains a comparator implemented by the MOS transistors M1-M7 and resistors R2,,,R3 . CMOS CL consumes the current I and introduces a capacitance Cin . The capacitance Cout represents the load caused by the interface circuitry. A low potential output signal of OVD corresponds to CL output validity. A high potential output signal corresponds to CL output invalidity. So, OVD generates OV signal in negative logic manner.
The transfer characteristics of CVC is determined by a system of three equations:
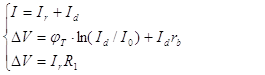
![]()
where I is an input current of CVC, V is a voltage drop on the CVC circuit, Ir is a current flowing through the resistor R1, Id is a current passing through the diode D1, I0 is a leakage current of the diode, rb is a bulk resistance of the diode. Here ![]() stands for kT/q where k is Boltzmann's constant, T is absolute temperature, q is charge of an electron.
stands for kT/q where k is Boltzmann's constant, T is absolute temperature, q is charge of an electron.
Equations (1)-(3) determine the functional connection F between input current I and voltage drop V: ![]() . Graphic solution of the system is shown in Fig.10.
. Graphic solution of the system is shown in Fig.10.
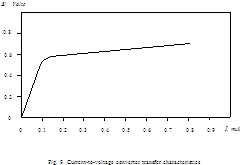
CVC parameters to be calculated are R1 and rb. Initial data for calculating R1 are the threshold voltage drop Vth and corresponding threshold input current Ith . Value Ith is determined by minimal current consumed by CMOS CL in transient state. Initial data for calculating rb are maximal voltage drop Vmax and corresponding maximal input current Imax. Value Imax is determined by the maximal number of gates in CL switching simultaneously and their load capacitances.
The comparator chosen is the CMOS ECL receiver proposed by Chappell et al.(11). The circuit includes a single differential amplifier stage with built-in compensation for parameter variations, followed by a CMOS inverter. The comparator has 100-mV worst-case sensitivity in 1-m technology. Detailed static and dynamic analysis of the comparator circuit was given in (11).
The comparator compares input voltage signal Vin with reference voltage Vref. If Vin <Vref the comparator output signal equals to logical zero which means that CL outputs are valid. Otherwise, Vin >Vref, the comparator output signal equals to logical "one" which means that the outputs are invalid.
As it follows from the OVD circuit configuration,
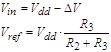
![]()
where Vdd is a voltage of power supply.
Equations (4) and (5) allow us to calculate the threshold voltage drop V of the CVC circuit:
since ![]() , so
, so ![]()
![]()
If 0<V<500mV then the diode D1 of CVC operates in the very small current region Id 0 and Id <<Ir. So the component Id in the Equation (1) can be neglected and IIr =V/R1 .
For practical values of ![]() the threshold input current of the OVD circuit is reversely proportional to the resistance of R1 :
the threshold input current of the OVD circuit is reversely proportional to the resistance of R1 : ![]() . Substituting Equation (6) yields
. Substituting Equation (6) yields
![]() .
.
As to choosing value of r it must be done with regard to maximal voltage drop Vmax .
If V>750mV, the diode D1 is in active mode and while r <<R1 the condition Ir <<Id is true. So, in the large current region IId and Equation (2) determines an almost linear dependence between I and V. For instance, if the maximal voltage drop Vmax =900mV and maximal input current Imax=2mA, then in accordance with the Equation (2) r 100. Typical element values for the OVD circuit with Vth =400mV are given in Table 1.

The turn-on ton and turn-off toff delays of the OVD circuit depend on the OVD itself and the CMOS CL as well. (Switching the OVD output from low to high voltage is called "turning-on" and reverse switching is called "turning-off".)
Consider a piece of CMOS CL and its interaction with OVD circuit (Fig.11). The piece is an SPP including N logic gates. Each gate is shown symbolically as a connection of PMOS and NMOS networks. All the capacitances affecting ton and toff can be brought down to three components:
(i) CLi is the load capacitance of the i-th gate;
(ii) Cpsi is the power supply bus capacitance associated with the i-th gate;
(iii) Cin is the input capacitance of the OVD circuit.

Let i is a probability of the i-th gate being in the state of high output potential. In this state the capacitance CLi is connected with power supply bus through the low channel resistance of turned-on transistors in PMOS network of the i-th gate. Then equivalent capacitance Ceq connected to the OVD circuit input equals
![]() (7)
(7)
where N is a number of gates in the considered SPP. Here the resistance of conducting PMOS network is assumed to be negligible.
Equation (7) is also true for CL including several SPPs. In that case summing must be carried out for all the gates belonging to CL.
Simulation shows that ton and toff are proportional to the OVD time constant =R1Ceq. It was also obtained that when N>20, the component under the sign of summation in Equation (7) can be much larger than the component Cin. Due to voltage drop V the effective power supply voltage is reduced and CL performance is decreased by about 35 percent (7).
In order to make SIM operating faster special attention must be paid to reducing the capacitance introduced by CL.
4.3 Speed-independent address bus
The simplest case of CL is a scheme degenerated into a set of wires called a multi-bit bus. Let us develop the OVD circuit for such a CL.
Multi-bit bus consists of several lines. Each line can be considered as a medium for signal propagating from one end of the chip to another. Delay of signal propagation through a line depends on several factors:
(a) output impedance and symmetry of driver circuit;
(b) initial state of the line: if driver is symmetrical, line switching from high to low voltage lasts shorter than reverse switching;
(c) electrical properties of the line as a signal propagation medium (resistance of conducting layer and capacitances between the line and other wires next to it);
(d) length of the line;
(e) input impedance and sensitivity of receiving circuit.
Since different lines of the bus operate in different conditions (a)-(e), signal propagation delays are different, too. From the standpoint of environment the bus behaves like any other more complicated CL.
Asynchronous RAM designers use a bus transition detector since 1980s (13-15). Such a detector is usually based on double-rail address coding and two series connected transistors for each address bit (15). One of the transistors receives the true address signal and the other receives the complementary address signal of the particular address bit. For any steady state condition one of the transistors will be turned on and one will be turned off. There will be a finite rise and fall time during a transition of the address bit. There is a short time during which both transistors are conducting. The establishment of the conductive path provides the detection of the address transition. In the first asynchronous RAMs the output signal of the transition detector is used for bit line precharging and for enabling/disabling sense amplifiers and peripheral circuitry.
Self-timed RAM announced in 1983 (14) used transition detectors not for address transition only but also for detecting read/write completion and address/bit line precharge completion as well.
The CMOS transition detector was invented in 1986 (15). This circuit is also based on double-rail coding and uses a pair of series-connected NMOS transistors (Fig.12). The scheme for -bit bus control contains line transition detectors (LTDs) and AND-gates. Outputs of AND-gates are united in node M forming wired OR. The output inverter serves as a pulse shaper. Capacitors C1 and C2 are intended to prolong rise time of the LTD output signal (true and complementary). This is necessary for reliable detection.

The main drawback of the circuit is speed dependence. One can see that if true and complementary address bit signal have different propagation delays, the conducting path via NMOS transistors will never be formed.
Using the OVD circuit proposed in Section 4.2 as LTD we can avoid this drawback.
Note that address transmission through the address bus is unidirectional. So to detect completion of bus transition it is enough to recognize the bus state at the destination end. For this purpose we modify CL to consist of lines. The modification means introducing LTDs, each actually a CMOS inverter chain. Each chain contains two inverters loaded with a capacitance (Fig.13). Input of each LTD is connected with corresponding line of the bus at the destination end. Power supply pads of all LTDs are connected to the current input of the same OVD circuit.

The parameters of the input current signal for the OVD circuit are varied by
(i) value of capacitances C1 and C2 ;
(ii) dimensions of MOS transistors M1 -M4 .
Since all transitions in CL are of the same duration and can be lengthened to be outlast the OVD turning-on time, we simplify the interface circuitry by disallowing the asymmetrical delay.
Due to short duration of normal transition in this CL we must take into account the integral nature of the sensitivity of the OVD circuit. OVD sensitivity depends on both amplitude and width of input current pulse. Simulated operation region of the OVD circuit for current pulses shorter than 30ns is shown in Fig.14. It is obvious that in this case the threshold of the OVD circuit must be determined by threshold charge Qth value. The OVD input charge Q equals to 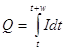 where I is OVD input current, t is a moment of time when transition occurs, w is a width of input current pulse. Turning-on condition for the OVD circuit is Q=Qth.
where I is OVD input current, t is a moment of time when transition occurs, w is a width of input current pulse. Turning-on condition for the OVD circuit is Q=Qth.

When the LTD circuit shown in Fig.13 is used, the charge value Q is determined by either C1 or C2. Namely, if the line goes from low to high voltage, Q=VC2. If the line goes in the reverse direction then ![]() where V is charging/discharging voltage, approximately equal to the effective power supply voltage: VVdd -V. Here Vdd is OVD power supply voltage and V is CVC voltage drop.
where V is charging/discharging voltage, approximately equal to the effective power supply voltage: VVdd -V. Here Vdd is OVD power supply voltage and V is CVC voltage drop.
The OVD circuit with typical parameters (See Table 1) has a threshold charge value Qth =4.010-12 C. When C1 =C2 =CL , the minimal value of CL providing OVD capacity for operation is about 1.010-12 F.
Influence of transistors M1 -M4 dimensions on LTD delay d is determined by approximation (17):

where ~ is a sign of proportionality, G and G are the conductances of NMOS and PMOS transistors respectively (CL =C1 =C2.)
Since ![]() and
and ![]() where W and L are width and length of transistor channels of the corresponding conduction type, the LTD delay d is proportional to
where W and L are width and length of transistor channels of the corresponding conduction type, the LTD delay d is proportional to ![]() .
.
It has been obtained that for ![]() ,
, ![]() , CL=1.0pF and Vdd-V=5.0V the LTD delay d=7.6ns.
, CL=1.0pF and Vdd-V=5.0V the LTD delay d=7.6ns.
When LTD works jointly with the OVD in the speed-independent bus, the real value of the LTD delay will increase by 30-40 percent due to OVD's R1 effect on the effective power supply voltage.
To determine the appropriate value of R1 in the OVD circuit we must know threshold input current Ith corresponding to threshold voltage drop Vth recommended to be equal to 400mV.
Average input current Iav in transient state of one line is determined by the expression Iav =CLv where v is the average rate of increase in the output signal for an inverter included in LTD. For typical values v=1.0109 Volts per second and CL =1.0pF, Iav =1.0mA. Accepting Ith =0.4mA and Imax=2.0mA we obtain R1=1k and r=100.
Simulation has shown that in this case OVD turning-on delay can be approximated by an empirical expression:
ton(ns)=8.1+0.1
where is the address bus bit capacity. Total delay of recognizing address transition ttot =dg+ton where g is a coefficient of the LTD delay increase due to reducing power supply voltage. As we showed above g1.35. It can be seen that if =32, ttot=21.6ns.
4.4 Speed-independent adder
The circuit we use in this Section as a CL was a touch-stone for many speed-independent circuit designers for about four decades. We mean a ripple carry adder (RCA) which is actually a chain of one-bit full adders (Fig.14).
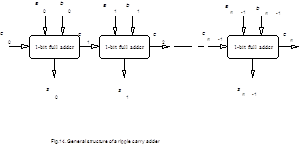
Each full adder calculates two Boolean functions: sum i=aiici and output carry ci+1=aii+bici+aici where ai, i are summands, ci is input carry and stands for XOR operation.
In 1955 Gilchrist et al. proposed speed-independent RCA with carry completion signal (18). In 1960s that circuit was carefully analyzed and improved (19-21). In 1980 Seitz used RCA for illustrating his concept of equipotential region and his approach to self-timed system design (4).
Now we use RCA as a CL for illustrating our approach to SIM design.
As it was shown in Section 4.2 the turn-on and turn-off delays of the OVD circuit are proportional to the equivalent capacitance Ceq associated with OVD circuit input. Capacitance Ceq depends linearly on a number of gates N in CMOS CL. To speed up a SIM it is necessary to reduce a number N. This can be reached by structural decomposition CMOS CL into subcircuits CL1, CL2, etc. Each subcircuit CLi is connected to its own detecting circuit OVDi or directly to the power supply if this subcircuit transition does not affect the transition duration in CL as a whole. Each detecting circuit OVDi generates its own OV signal which is combined with other OVDs' output signals via a multi-input OR (NOR) element. The output signal of that element serves as OV signal of the CMOS CL.
Multi-bit RCA computation time is determined by length of maximal activated carry chain. A lot of papers were devoted to analysis of carry generation and carry propagation in RCA (19-21), many of them contained their own methods for estimation or calculation of average maximal activated carry chain. We do not intend to add another one.
Let us have a look inside RCA. As it was mentioned above RCA consists of one-bit full adders and each full adder consists of two parts: forming sum i part and forming carry ci+1 part (Fig.16).
In multi-bit RCA all forming sum parts do not interact with each other and do not affect on transition duration in RCA. Each forming carry ci+1 part receives ci signal from preceding forming carry part and sends ci+1 signal to consequent one.
To decompose RCA we use three heuristic tricks:
(i) All forming sum parts we connect directly to power supply.
(ii) We divide each forming carry part into three subcircuits denoted in Fig.16 by numbers 1,2 and 3. All subcircuits 1 we connect directly to power supply because they do not contain input ci and so do not contain carry propagation path.
(iii) All subcircuits 2 we connect to OVD1 and all subcircuits 3 we connect to OVD2. Outputs of OVD1 and OVD2 are connected to two-input NOR-gate forming RCA OV signal in positive logic manner (Fig.17).
OVD1 and OVD2 input currents I1 and I2 curves for 6-bit RCA and longest transition duration are shown in Fig.18.
Accepting Vth1,2=400mV we calculated the OVD circuits parameters. It was obtained R11=5k, Ith1=0.08mA, R12=3k, Ith2=0.13mA. OVD1 and OVD2 delay dependencies on a number of bits in RCA are shown in Fig.19.
4.5 Comparison of SIMs with synchronous counterparts
Transition duration in CL is a random variable. Probability of transition with duration D is determined by implemented Boolean function and distribution of input logical combinations. Domain of possible values for variable D occupies the interval (0;Dmax). Here Dmax is a length of critical path in CL.
Let ![]() is a mathematical expectation of transition duration in CL where Di is a length of i-th SPP in CL, i is a probability of i-th path being the longest activated SPP.
is a mathematical expectation of transition duration in CL where Di is a length of i-th SPP in CL, i is a probability of i-th path being the longest activated SPP.
When CL works in the synchronous mode, the cycle duration T is chosen with regard to maximal transition duration Dmax. Certain margin must be added to Dmax to provide reliable operation of CL in the case of CL parameter variations: T =kDmax where k is a margin coefficient.
In SIM cycle duration is a random variable with expectation Tsi = gDme+toff+tif where g is a coefficient of CL delay increasing due to reducing power supply voltage, toff is turn-off delay of the OVD circuit, tif is an interface circuitry delay.
We determine efficiency E for speed-independent mode of CL operation as relative increase of SIM performance in comparison to its synchronous counterpart:![]() .
.
Generally, speed-independent mode is more efficient than synchronous one if T >Tsi or, in other words, ![]() .
.
In the case of RCA ![]() where tc is a delay of carry forming part, is a number of full adders in RCA.
where tc is a delay of carry forming part, is a number of full adders in RCA.
It has been shown (19) that in -bit RCA Dmetclog2(5/4). Then, in the case of speed-independent operation Tsi=gtclog2(5/4)+toff+tif.
We have obtained dependencies of T, Tsi on a number of bits in RCA that are shown in Fig.20. As it can be seen, speed-independent operation of RCA is more efficient while >8.
5.Conclusion
6.Acknowledgement
I would like to thank Igor Shagurin and Vlad Tsylyov of the Moscow Physical Engineering Institute for helpful discussions of this work. I am also grateful to Chris Jesshope of University of Surrey and Mark Josephs of Oxford University who kindly provided the latest material on their research in the area of delay-insensitive circuit design.
References
(1) Miller, R.E., Switching theory (Wiley, New York, 1965), vol.2, Chapter 10.
(2) Unger, S.H., Asynchronous Sequential Switching Circuits (Wiley, New York, 1969).
(3) Armstrong, D.B., A.D. Friedman, and P.R. Menon, Design of Asynchronous Circuits Assuming Unbounded Gate Delays, IEEE Trans.on ComputersC-18 (12) (1969) 1110-1120.
(4) Seitz, C.L., System timing, in: C.A. Mead and L.A. Conway, eds., Introduction to VLSI Systems (Addison-Wesley, New York, 1980), Chapter 7.
(5) Izosimov, O.A., I.I. Shagurin, and V.V. Tsylyov, Physical approach to CMOS module self-timing, Electronics Letters26 (22) (1990) 1835-1836.
(6) Veendrick, H.J.M., Short-circuit dissipation of static CMOS circuit and its impact on the design of buffer circuits, IEEE J. Solid-State Circuits SC-19 (4) (1984) 468-473.
(7) Chappell, B.A, T.I. Chappell, S.E. Schuster, H.M. Segmuller, J.W. Allan, R.L. Franch, and P.J. Restle, Fast CMOS ECL receivers with 100-mV worst-case sensitivity, IEEE J. Solid-State CircuitsSC-23 (1) (1988) 59-67.
(8) Chu, S.T., J. Dikken, C.D. Hartgring, F.J. List, J.G. Raemaekers, S.A. Bell, B. Walsh, and R.H.W. Salters, A 25-ns Low-Power Full-CMOS 1-Mbit (128K8) SRAM, IEEE J. Solid-State CircuitsSC-23 (5) (1988) 1078-1084.
(9) Frank, E.H., and R.F. Sproull, A Self-Timed Static RAM, in: Proc. Third Caltech VLSI Conference (Springer-Verlag, Berlin, 1983) pp.275-285.
(10) Donoghue, W.J., and G.E. Noufer, Circuit for address transition detection, US Patent 4563599, 1986.
(11) Huang, J.S.T., and J.W. Schrankler, Switching characteristics of scaled CMOS circuits at 77K, IEEE Trans. on Electron DevicesED-34 (1) (1987) 101-106.
(12) Gilchrist, B., J.H. Pomerene, and S.Y. Wong, Fast Carry Logic for Digital Computers, IRE Trans. on Electronic ComputersEC-4 (4) (1955) 133-136.
(13) Hendrickson, H.C., Fast High-Accuracy Binary Parallel Addition, IRE Trans. on Electronic Computers EC-9 (4) (1960) 465-469.
(14) Majerski, S., and M. Wiweger, NOR-Gate Binary Adder with Carry Completion Detection, IEEE Trans. on Electronic ComputersEC-16 (1) (1967) 90-92.
(15) Reitwiesner, G.W., The determination of carry propagation length for binary addition, IRE Trans. on Electronic ComputersEC-9 (1) (1960) 35-38.