Решение обратной задачи вихретокового контроля

Содержание

1. Техническое задание

Разработать алгоритм решения обратной задачи вихретокового контроля (ВТК). Объектом контроля (ОК) являются проводящие немагнитные листы. Объекты контроля подвергаются термообработке (закалка, отпуск) или насыщению внешних слоев различными веществами, что приводит к изменению механических, а вследствие этого и электромагнитных свойств материала листа по глубине.

Задача заключается в определении, в рамках допустимой погрешности, зависимости электропроводности (ЭП) от глубины (Н) в ОК для данного состояния. Метод контроля заключается в измерении определенного количества комплексных значений вносимой ЭДС на различных частотах с помощью накладного вихретокового преобразователя (НВТП).

Необходимо выбрать математическую модель задачи, способ аппроксимации искомого решения, рассмотреть алгоритм решения.

Используя программную реализацию, исследовать поведение погрешности аппроксимации зависимости (Н) от следующих факторов:

1. От величины приборной погрешности измерения ЭДС

2. От вида зависимости электропроводности от глубины (Н)

3. От параметров аппроксимации решения

4. От диапазона частот возбуждения ВТП

2. Анализ технического задания.

Основная задача вихретокового контроля с помощью накладных преобразователей состоит из двух подзадач:

• Прямой задачи расчета вносимой ЭДС в присутствии немагнитного проводящего листа с произвольной зависимостью ЭП по глубине.

• Обратной задачи нахождения зависимости ЭП как функции глубины в немагнитном проводящем листе по результатам измерений определенного количества комплексных значений вносимой ЭДС.

2.1 Прямая задача ВТК

Полагая зависимость ЭП от глубины известной проведем ее кусочно-постоянную аппроксимацию. Это позволяет свести исходную задачу к расчету ЭДС в многослойном листе, в каждом слое которого ЭП принимает постоянное значение.

Как показано в работе (50), подобная модель вполне адекватно описывает задачу и дает отличное согласование с результатами опытов.

Рекуррентные формулы для произвольного количества слоев хорошо известны (1-5,36, 42,43,50-52). Таким образом решение прямой задачи в рамках принятой модели затруднений не вызывает.

2.2 Обратная задача ВТК

С математической точки зрения обратная задача ВТК относится к классу некорректных задач(49) и ее решение неустойчиво т.е. при сколь угодно малой погрешности исходных данных( набора измеренных вносимых ЭДС ) погрешность решения ( рассчитанных локальных значений ЭП ) может быть сколь угодно большой, а одному набору измерений может отвечать много (формально бесконечно много) распределений ЭП по глубине.

При попытке расчета некорректной задачи как корректной, вычислительный процесс за счет неустойчивости сваливается в заведомо худшую сторону. В нашем случае это означает получение распределения ЭП, которое, хотя и обеспечивает требуемое совпадение измеренной и вычисленной ЭДС, но является явно нереальным из-за осцилляций. Следует отметить, что амплитуда и частота осцилляций распределения ЭП растут при увеличении числа независимых параметров аппроксимации ЭП ( коэффициентов полинома в случае полиномиальной аппроксимации, количества узлов при сплайн-аппроксимации и т.д.).

При наличии погрешности измерения вносимой ЭДС, превышающей на несколько порядков вычислительную погрешность и на практике составляющей не менее (0.5-1)% от измеряемого сигнала, ситуация значительно осложняется.

Учитывая вышеизложенное для выделения из множества допустимых распределений решения, наиболее удовлетворяющего физической реальности, в алгоритмах решения обратной задачи необходимо использовать дополнительную априорную информацию. На практике это реализуется введением некоторых критериев, позволяющих отличить решение, отвечающее практике, от физически нереального.

Для решения обратной задачи ВТК предлагались три возможные стратегии(46):

1. Решение большого числа прямых задач и табуляция результатов для различных моделей. Измеренные данные с помощью некоторых критериев сравниваются с таблицей. Подход очень экстенсивный и требующий проведения избыточного числа расчетов, поэтому на практике встречающийся редко.

2. Условная минимизация невязки измеренных и расчитанных данных. Очень мощный и универсальный метод, широко распространен для решения обратных задач в различных областях техники (41,44,49). Позволяет восстанавливать произвольное распределение ЭП по глубине (вообще говоря произвольное 3D распределение), но требуется довольно сложная процедура расчета.

3. Аналитическое инвертирование ядра оператора и использование алгоритма, зависящего от ядра уравнения(46). Потенциально самый малозатратный метод, однако как и все аналитические, применим далеко не всегда.

В нашем случае остановимся на втором подходе, поскольку он сочетает в себе универсальность, точность и относительную простоту реализации.

В целом процесс решения обратной задачи сводится к итерационному решению прямой задачи для текущей оценки распределения ЭП и внесению изменений в эту оценку в соответствии с величиной невязки.

2.3 Модель задачи

Приведем основные положения, на основе которых будет построена модель нашей задачи:

• ОК представляет из себя находящуюся в воздухе проводящую пластину толщиной Н состоящую из N плоско-параллельных слоев толщиной _i.

• В пределах каждого слоя удельная электропроводность имеет постоянное значение т.е. распределение по глубине аппроксимируется кусочно-постоянной зависимостью.

• Возбуждающая и измерительная обмотки ВТП заменяются нитевидными моделями. Следует отметить, что это предположение сказывается лишь на решении прямой задачи, а проведя интегрирование можно получить выражения для катушек конечных размеров.

• Для численного моделирования реальных распределений ЭП применим пять типов аппроксимации: сплайном, кусочно-постоянную, кусочно-линейную, экспоненциальную и гиперболическим тангенсом. В процессе решения прямой задачи с их помощью вычисляются значения в центральных точках слоев пластины.

2.4 Анализ литературы

2.4.1 Зарубежные методы решения

Решению обратной задачи ВТК посвящен ряд работ в зарубежных изданиях. Следует отметить монографию (38), в которой рассмотрены случаи импульсного возбуждения, а оперируют в частотной и временной областях напряженностью электрического поля.

Подход к решению квазистационарных задач рассмотрен в цикле статей (45-51). Он основан на интегральной постановке задачи с помощью функций Грина(31-34,39). Для иллюстрации рассмотрим решение обратной задачи ВТК согласно (49).

А. Прямая задача

Определим функцию v(r)=( (r) - ₀ )/₀ , где (r)- произвольное распределение проводимости, а ₀ - ее базовая величина. Функция v(r)может представлять собой как описание произвольного распределения проводимости (в этом случае для удобства полагаем (r)=₀ вне некоторого ОК объема V, тогда v(r) отлична от нуля только в пределах V ) так и некоторого дефекта (для трещины v(r)=-1 внутри дефекта и равна нулю вне его).

Рассмотрим систему уравнений Максвелла в предположении гармонического возбуждения exp(-jwt) и пренебрегая токами смещения:

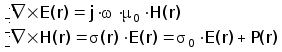
( 2.4.1)

где P(r)=( (r)-₀ )ЧE(r)=₀Ч v(r)ЧE(r) - может интерпретироваться как плотность диполей эффективного тока, причиной которого является вариация (r)-₀.

Решение уравнений Максвелла можно представить в виде

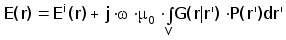
( 2.4.2)

где Eⁱ(r) - возбуждающее поле, а G(r|r’) - функция Грина, удовлетворяющая уравнениюСґСґ G(r|r’)+k²Ч G(r|r’)=d(r-r’) , k²=-jЧwЧm₀Чs₀ , d(r-r’)- трехмерная дельта-функция.

Импеданс ВТП можно выразить как

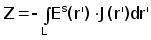
( 2.4.3)

где интеграл берется по измерительной катушке, J(r) - плотность тока в возбуждающей катушке. Применяя теорему взаимности импеданс можно представить через возбуждающее поле:

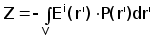
( 2.4.4)

где интеграл берется по объему ОК.

В. Обратная задача

Пусть v(r) - оценка истинной функции v_true(r), Z_obs(m) - измеренный импеданс ВТП в точке r₀ на частоте возбуждения w , m=(r₀,w) - вектор в некоторой области определения M , Z(m,v) - оценка величины Z_obs(m) на основе решения прямой задачи.

Определим функционал невязки измеренных и рассчитанных значений импеданса ВТП как :

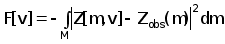
( 2.4.5)

Предположим, что для решения обратной задачи используется итерационный алгоритм типа метода спуска: v(r)= v^n-1(r)+a(r). Можно показать, что в случае метода наискорейшего спуска итерация имеет вид: v(r)= v^n-1(r)-aЧСF( v^n-1(r) ), где градиент функционала СF(v) можно определить как :

( 2.4.6)

где Re обозначает вещественную часть, * обозначает комплексную сопряженность.

Требуемый в (2.4.6) градиент импеданса можно определить как:

СZ(r) = -s0ЧE(r)ЧE*(r)

( 2.4.7)

где E^*(r) - решение уравнения

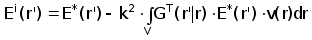
( 2.4.8)

С. Аппроксимация при решении обратной задачи

Пусть электропроводность моделируется с помощью конечного числа переменных (например узловых значений некоторой аппроксимации), а вектор р состоит из этих переменных. Тогда выражение (2.4.7) принимает вид:

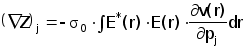
( 2.4.9)

где (СZ)_j - j-ая компонента градиента импеданса.

Значение j-ой компоненты градиента невязки (2.4.6) можно представить как:

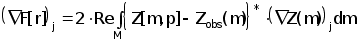
( 2.4.10)

Следует обратить внимание на то, что в случае дискретного пространства М (конечное число измерений) интеграл в (2.4.10) заменяется суммой.

С учетом приведенных преобразований итерация метода наискорейшего спуска принимает вид:

pjn = pjn-1 - aЧ(СFn-1)j

( 2.4.11)

где - номер итерации.

D. Пример применения

В качестве примера рассмотрим функцию v(r) в виде v(r)=Sc_iЧf_i(r), i=1,N , где f_i(r) - множество линейно независимых базовых функций с коэффициентами c_i. Рассматривая коэффициенты c_i в роли параметров аппроксимации (c_i=_i) получим из (2.4.9) для компонентов градиента импеданса:

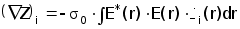
( 2.4.12)

В случае проводящего ОК, состоящего из N параллельных слоев с проводимостью _j распределение электропроводности по глубине можно представить с помощью функций Хевисайда H(z) как (z)=S_jЧ(H(z-z_j)-H(z-z_j+1)).

Подставляя в (2.4.12) базовые функции вида f_i(z)=(H(z-z_j)-H(z-z_j+1)), получим окончательное выражение:

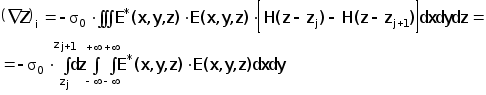
( 2.4.13)

Отметим основное преимущество такого решения. Несмотря на определенную сложность вычислений при решении интегральных уравнений (2.4.2-2.4.8) для расчета градиента импеданса НВТП необходимо решить только две такие задачи.

2.4.2 Отечественные методы решения

Подход, в значительной мере аналогичный работам (45-51) был предложен в работе (41). Из-за небольшого объема в ней уделено недостсточное внимание вопросам практической реализации, объяснены не все обозначения и не приведены результаты численного моделирования. В целом это значительно снижает практическую ценность статьи. Приведем основные положения этой работы.

Прямая задача

Пусть круговой виток радиусом а с током I находится в точке P=P(r,j,z), jО(-,) вблизи немагнитного ОК, занимающего область V. Пусть ОК обладает электрической проводимостью =₀Чs(Р) являющейся произвольной функцией координат. Требуется по N измерениям величины э.д.с. определить как функцию координат точек PОV. Причем i-ое измерение э.д.с. будем проводить на i-ом измерительном круговом витке с координатами P_i=P_i(r,j,z) i=1,N при неизменных частоте и расположении возбуждающего витка.

В общем случае напряженность электрического поля Е определяется через векторный магнитный потенциал А, причем А = А₀ + А_вн, где А₀ - возбуждающий, а А_вн - вносимый потенциалы.

(2.4.14)

Вводя функцию Грина G(p,p₀) получим

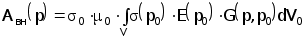
(2.4.15)

При этом вносимая напряженность электрического поля

Eвн = -jЧwЧAвн

(2.4.16)

Вносимая э.д.с., наводимая в i-ом витке

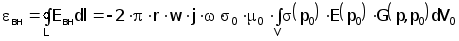
(2.4.17)

где функция Грина G(P,P₀) имеет вид

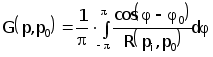
(2.4.18)

В дальнейшем рассмотрим случай, при котором V-полупространство (r>0,\j\<,z<0) с электрической проводимостью =₀Чs(Р), где (Р) - произвольная функция координаты z. В этом случае выражение (2.4.17) примет вид

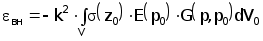
(2.4.19)

где k²=jwm₀₀ .

Для напряженности электрического поля Е(Р) справедливо представление

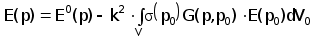
(2.4.20)

где Е⁰(р) - возбуждающее поле витка.

После проведения серии из N измерений величины e_вн выражение (2.4.19) дает связь между вносимыми ЭДС e_i и (z)E(r,z). Чтобы определить непосредственно =(z), находим E(r,z) при известной функции (z)E(r,z) из (2.4.20), после чего исключаем E(r,z) из известного.

Обозначим x()=-k²(z)E(r,z), а измеряемую совокупность ЭДС через Fi. Тогда (2.4.19) можно записать в операторной форме как

F = Px + d

(2.4.21)

где d - погрешность измерения.

Обратная задача

Построим функционал Ф(х)=||F-Px||²+a||x-x₀², где х₀ - некоторое известное ІблизкоеІ к искомому распределение, удовлетворяющее F₀=Px₀. Образуем вариацию функционала Ф(х), используя определение сопряженного оператора (Px,y)=(x,P*y). Для нахождения минимума Ф(х) приравняем его вариацию dФ нулю.

Вводя вспомогательную функцию u=x-x₀ и учитывая F₀=Px₀ проведем ряд преобразований. Искомое распределение (z) можно найти из равенства

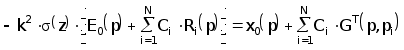
(2.4.22)

где напряженность электрического поля в точке р для известного распределения (z)имеет вид

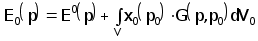
	(2.4.23)
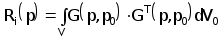
	(2.4.24)

Система алгебраических уравнений для определения коэффициентов С_i имеет вид

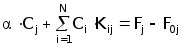
	(2.4.25)
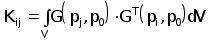, j=1,N	(2.4.26)

3. Прямая задача ВТК для НВТП

3.1 Уравнение Гельмгольца для векторного потенциала

Взаимодействие преобразователя с объектом контроля определяется системой уравнений Максвелла в дифференциальной форме(6) :

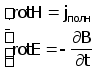
(3.1)

где

H	- вектор напряженности магнитного поля
E	- вектор напряженности электрического поля
B	- вектор магнитной индукции
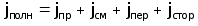
	- вектор плотности полного тока
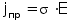
	- вектор плотности токов проводимости
s	- удельная электрическая проводимость
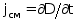
	- вектор плотности токов смещения
D	- вектор электрического смещения
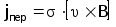
	- вектор плотности токов переноса
u	- вектор скорости переноса
jстор	- вектор плотности сторонних токов

Дополним систему (3.1) уравнениями связи:

B = mЧm0Ч H	(3.2)
B = rot A	(3.3)

где

m0 = 4ЧpЧ10-7	- магнитная постоянная
m	- относительная магнитная проницаемость
A	- векторный потенциал магнитного поля

Преобразуем систему уравнений (3.1) с учетом следующих предположений(4) :

• ОК неподвижен относительно электромагнитного поля т.е. jпер = 0

• среда изотропна и ее параметры не зависят от напряженностей полей

• воздействия синусоидальны

• последовательность дифференцирования по времени и пространственным координатам можно изменять, а операция дифференцирования линейна

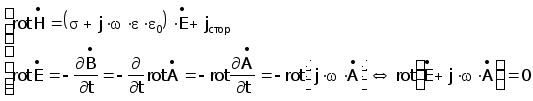
(3.4.1) (3.4.2)

Поскольку ротор градиента любого скаляра тождественно равен нулю, величину в скобках выражения (3.4.2) можно приравнять градиенту некоторого скаляра y , например скалярного потенциала электрического поля :

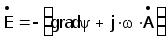
(3.5)

Заменяя векторы напряженности магнитного и электрического поля в (3.4.1) через векторный потенциал магнитного поля получаем :

grad div A - DA = -mЧm0 Ч ( s + jЧwЧeЧe0 ) Ч ( grady + jЧwЧA ) + mЧm0 Чjстор

(3.6)

Откуда после очевидных преобразований следует:

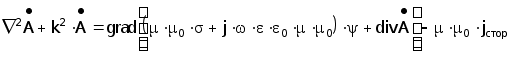
(3.7)

где

k2 = w2 ЧmЧm0 ЧeЧe0 - j ЧwЧmЧm0 Чs

(3.8)

Поскольку векторный потенциал магнитного поля задан с точностью до градиента некоторого скаляра, а потенциал y с точностью до постоянной величины, имеется возможность положить значение величины в квадратных скобках выражения (3.7) равное нулю (так называемая калибровка Лоренца). В результате получаем уравнение Гельмгольца для векторного потенциала магнитного поля :

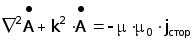
(3.9)

В дальнейших рассуждениях используем следующие предположения :

• Поле НВТП квазистационарно в том смысле, что волновыми процессами в воздухе можно пренебречь. Это вполне оправдано т.к. размеры НВТП и ОК обычно много меньше длины волны в воздухе, а потери на излучение по сравнению с потерями в ОК малы.

• В проводящем теле будем рассматривать только волновые процессы, обусловленные наличием параметров и m т.е. токами смещения( пропорциональными wЧeЧe0 ) как и в воздухе пренебрегаем. Легко показать, что это предположение справедливо не только для металлов, но и для полупроводниковых материалов с удельным сопротивлением r до 50(ОмЧсм). В этом случае выражение (3.8) принимает вид : .

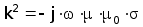3.2 Поле витка над многослойной средой

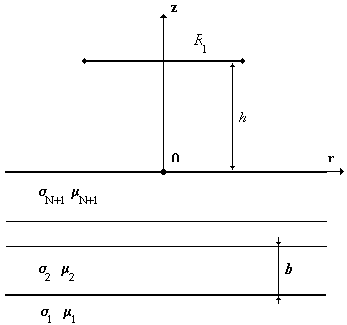
Введем цилиндрическую систему координат ( r,j,z ). Пусть : 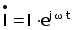- ток, протекающий по нитевидной возбуждающей обмотке с радиусом R1, находящейся на расстоянии h от N-слойной среды jстор = I Чd( z - h ) Чd(r - R1) Отметим, что в силу осевой симметрии системы

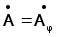
В цилиндрической системе координат выражение (3.9) имеет следующий вид :

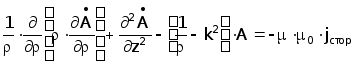
(3.10)

Применяя к (3.10) преобразование Фурье-Бесселя с ядром в виде функции Бесселя первого порядка имеющее вид :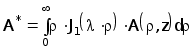 получаем

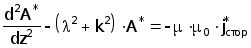
(3.11)

Так как на поверхностях раздела слоев ОК должна сохранятся непрерывность тангенциальных составляющих векторов напряженностей магнитного и электрического поля, дополняем уравнение (3.11) граничными условиями на поверхностях слоев ОК( граничные условия одинаковы для А и А* ) :

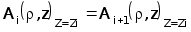
	(3.12)
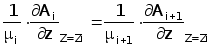
	(3.13)

Решив уравнение (3.11) с учетом граничных условий (3.12-3.13) и применяя к решению обратное преобразование Фурье-Бесселя имеющее вид : получаем для полупространства над ОК

где j=j( l , m , s ) - функция граничных условий.

3.3 Воздействие проводящего ОК на НВТП

Для большинства инженерных расчетов можно использовать нитевидную модель обмоток НВТП использованную в (п 3.2). При данном упрощении получаем :

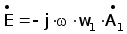
	- напряженность электрического поля	(3.15)
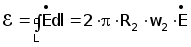
	- ЭДС наводимая в измерительной обмотке с радиусом R2 и числом витков w2	(3.16)

Анализируя формулу (3.14) можно заметить, что первый интеграл представляет собой векторный потенциал создаваемый возбуждающей обмоткой, а второй интеграл - векторный потенциал вносимый ОК. В практике ВТК обычно анализируются вносимые параметры НВТП (напряжение, импеданс) поэтому получим выражение для вычисления вносимого напряжение кругового трансформаторного накладного ВТП используя (3.15-3.16):

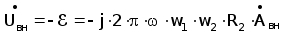
(3.17)

Подставляя выражение для вносимого векторного потенциала (3.14) в уравнение (3.17) окончательно получаем :

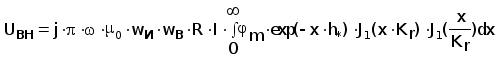
(3.18)

где

w = 2ЧpЧf	- круговая частота тока возбуждения I
m0	- магнитная постоянная
wи , wв	- числа витков измерительной и возбуждающей обмоток НВТП
R = Ц(RиЧRв)	- эквивалентный радиус НВТП
Kr = Ц(Rв/Rи)	- параметр НВТП
x	- переменная интегрирования
h* = (hи + hв)/2	- обобщенный зазор
J1	- функция Бесселя 1 рода 1 порядка
jm	- функция граничных условий

Функция граничных условий для m-слойного ОК с плоскопараллельными слоями может быть вычислена по рекуррентной формуле(2):

где

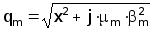
	(3.20)
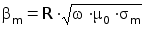
	(3.21)
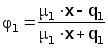
	(3.22)

th(z)	- гиперболический тангенс
mm	- относительная магнитная проницаемость m-го слоя
bm* = 2Чtm / R	- относительнаятолщина m-го слоя
tm	- толщина m-го слоя
qm	- обобщенный параметр m-го слоя
j1	- функция граничных условий для нижнего полубесконечного слоя, для воздуха ( m = 1 , e = 1 , = 0 ) j1 = 0

При анализе годографов для удобства используют нормированные зависимости. Для НВТП нормировку производят по модулю максимального вносимого напряжения, которое соответствует идеально проводящему ОК и вычисляется при j_м = -1:

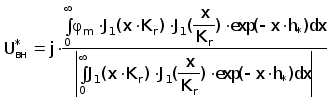
(3.23)

Такая нормировка обобщает полученные результаты, расширяет область их применения и делает их однозначными.

Отметим, что для получения часто используемого в ВТК значения импеданса НВТП достаточно разделить правую часть (3.18) на величину тока возбуждения I.

4. Обратная задача ВТК для НВТП

Решение обратной задачи ВТК состоит в нахождении зависимости (h) распределения электропроводности по глубине пластины используя набор из N измеренных с помощью НВТП вносимых напряжений. Математически обратную задачу можно представить интегральным уравнением

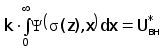
(4.1)

Поскольку явного метода решения уравнения (4.1) не существует, применим к нему метод квазирешения (п5.3.2). В постановке для локального в смысле Чебышева критерия получим корректную задачу минимизации функционала невязки:

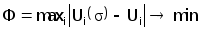, i=1,N

(4.2)

Учет априорной информации в обратной задачи ВТК удобно проводить в виде интервала ( s_min , s_max ), которому могут принадлежать значения электропроводности. В этом случае можно рассматривать задачу (4.2) как задачу нелинейного программирования вида:

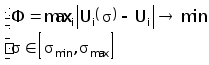
(4.3)

Заметим, что поскольку ограничения в задаче (4.3) являются линейными, разумным представляется применение метода условного градиента (п6.2.1). Рассмотрим процесс решения системы (4.3) в предположении, что электропроводность аппроксимируется по узловым значениям _j , j=1,M.

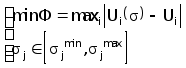
(4.4)

Линеаризуем функционал Ф в окрестности исследуемой точки ⁰ разложив его в ряд Тейлора с использованием только первых производных.

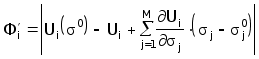
(4.5)

Пусть y = maxФ_i’ = Ф_p’ і 0. В этом случае мы можем свести задачу (4.4) к эквив